WHAT SHOULD BE ADDED TO THE POLYNOMIAL SO IT IS COMPLETELY DIVISIBLE

Problem 1 :

What must be subtracted from

p(x) = 8x⁴ + 14x³ - 2x² +7x -8

so that the resulting polynomial is exactly divisible by

g(x) = 4x² + 3x -2?

Solution :

If the polynomial is divisible by another polynomial, then the remainder will be 0.

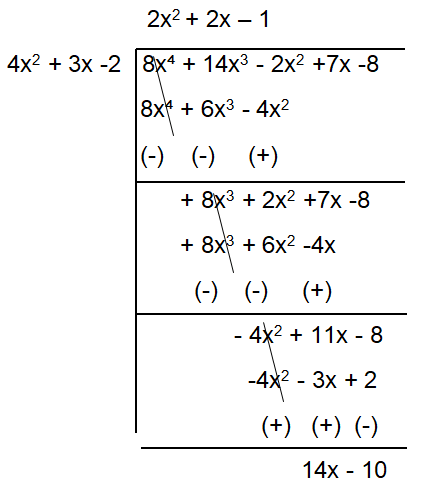
Since the remainder is 14x - 10, to get 0 as a remainder we have to subtract 14x - 10 from the given polynomial.

Problem 2 :

What must be added to

f(x) = 4x⁴ + 2x³ -2x² + x - 1

so that the resulting polynomial is divisible by

g(x) = x² +2x - 3?

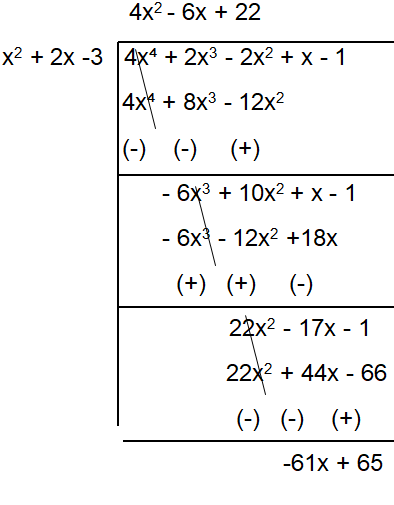
To make the remainder as 0, we need 61x - 65.

So, 61x - 65 to be added to the polynomial.

Problem 3 :

If the polynomial

x⁴ + 2x³ + 8x² + 12x + 18

is divided by another polynomial x²+5, the remainder comes

out to be px + q. Find the values of ' p' and ' q'?

Solution :

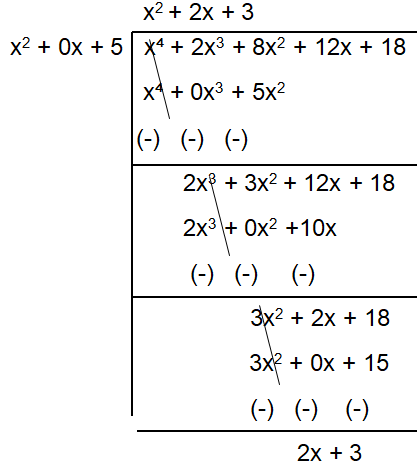
Remainder = 2x + 3

Comparing with the given remainder px + q

p = 2 and q = 3