WHAT NUMBER SHOULD BE MULTIPLIED OR DIVIDED TO MAKE PERFECT CUBE

Problem 1 :

What least number is to be multiplied with 3087 in order to get a perfect cube?

Solution :

Prime factorization of 3087 is,

3087 = 3 × 3 × 7 × 7 × 7

= 7³ × 3²

Hence, the smallest number by which 3087 must be multiplied to obtain a perfect cube is 3.

Problem 2 :

What is the least number by which 12800 should be divided in order to get a perfect cube?

Solution :

12800 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5

= 2⁹ × 5²

12800 is divided by 25 perfect cube is 512.

So, the cube root is 8.

Problem 3 :

Find the smallest common multiple of 48, 72 and 32 that is a perfect cube. 

Solution :

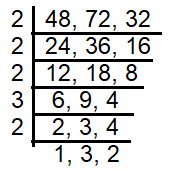
LCM (48, 72, 32) = 2 x 2 x 2 x 3 x 2 x 3 x 2

= 288

Decomposing 288, we get

= 2 x 2 x 2 x 3 x 3 x 2 x 2

To make it as perfect cube, we need one more 2 and one more 3.

So, the smallest number to be multiplied is 6.

Problem 4 :

By which least number should 72000 be multiplied such that the result is a perfect cube?

Solution :

Decomposing 72000, we get 

72000 = 72 x 10 x 10 x 10

= 2 x 2 x 2 x 3 x 3 x 10 x 10 x 10

To group the values, we need one more 3.

So, 3 is the least number to be multiplied to make it is perfect cube.

Problem 5 :

By which least number should 171500 be divided such that the result is a perfect cube ?

Solution :

171500 = 5 x 7 x 7 x 7 x 5 x 2 x 5 x 2

= 5³ x 7³ x 2²

So, the smallest number to be multiplied to make it as prefect cube is 2.

Problem 6 :

The least perfect square, which is divisible by each of 21, 36 and 66 is :

a)  213444   b)  214344   c)  214434    d) 231444

Solution :

The least common multiple of 21, 36 and 66 

= 3 x 7 x 7 x 6 x 11

= 3 x 7 x 7 x 2 x 3 x 11

= 2 x (7 x 7) x (3 x 3) x 11

The new numbers to be included are 2 and 11.

= (2 x 2) x (7 x 7) x (3 x 3) x (11 x 11)

= (2² x 7² x 3² x 11²)

= 4 x 49 x 9 x 121

= 213444

Problem 7 :

The least perfect square, which is divisible by each of 3, 4, 5, 6 and 8 is :

a)  900   b)  1200   c)  2500    d) 3600

Solution :

The least common multiple of 3, 4, 5, 6 and 8.

= 2 x 2 x 3 x 5 x 2

= 2² x 3 x 5 x 2

To make it as perfect square, the numbers 2, 3 and 5 to be included.

= 2² x 3 x 3 x 5 x 5 x 2 x 2

= 2² x 3² x 5² x 2²

= 4 x 9 x 25 x 4

= 3600

The required number is 3600.

Problem 8 :

The least number by which 294 must be multiplied to make it a perfect square is 

a)  2           b)  3         c)  6        d) 24

Solution :

294 can be decomposed as product of prime factors.

294 = 2 x 7 x 3 x 7

= 2 x 7² x 3

To make it as perfect square, the numbers to be included are 2 and 3.

= 2 x 2 x 7² x 3 x 3

= 2² x 7² x 3²

So, the required numbers to be included is 6. Option c is correct.

Problem 9 :

The square root of (7 + 3√5) (7 - 3√5) is 

a)   √5      b)  2      c) 4     d)  3√5

Solution :

First let us multiply these two binomials, and then take a square root.

= (7 + 3√5) (7 - 3√5)

Looks like (a - b)(a + b) = a² - b²

Here a = 7 and b = 3√5

= 7² - (3√5)²

= 49 - 9(5)

= 49 - 45

= 4

Square root of 4 is = √4

= 2

So, option b is correct.