VOLUME OF 3D SHAPES WHEN BASE AREA IS GIVEN

Calculate, to 3 significant figures, the volume of :

Problem 1 :

Solution :

Given, base area = 142.3 cm²

Height = 24.9 cm

Volume of pyramid = 1/3 × base area × height

= 1/3 × 142.3 × 24.9

= 3543.27/3

V = 1181 cm³

Problem 2 :

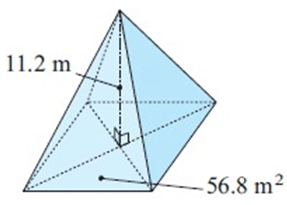
Solution :

Given, base area = 56.8 m²

Height = 11.2 m

Volume of pyramid = 1/3 × base area × height

= 1/3 × 56.8 × 11.2

= 636.27/3

V = 212 m³

Problem 3 :

Solution :

Given, base area = 14.2 cm²

Height = 7.8 cm

Volume of cone = 1/3 × base area × height

= 1/3 × 14.2 × 7.8

= 110.76/3

V = 36.9 cm³

Problem 4:

Solution :

Radius of hemisphere = 4.8 cm

Volume of hemisphere = 2/3 × πr³

= 2/3 × 22/7 × (4.8)³

= 4866/21

V = 230 cm³

Problem 5 :

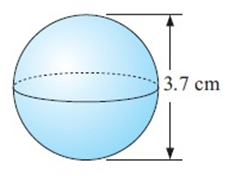
Solution :

Given, diameter of sphere = 3.7 cm

Radius r = 3.7/2 = 1.85 cm

Volume of sphere = 4/3 × πr³

= 4/3 × 22/7 × (1.85)³

= 557/21

V = 26.5 cm³

Problem 6 :

Solution :

Given, base area = 4.2 m²

Height = 1.87 m

Volume of cone = 1/3 × base area × height

= 1/3 × 4.2 × 1.87

= 7.85/3

V = 2.62 cm³

Problem 7 :

Solution :

Given, length = 2.8 cm

Width = 1.7 cm

Height = 2.9 cm

Volume of rectangular based pyramid = 1/3 × length × width × height

= 1/3 × 2.8 × 1.7 × 2.9

= 13.80/3

V = 4.60 cm³

Problem 8 :

Solution :

Given, base = 8.9 cm

Height = 6.8 cm

Area of base triangle = 1/2 × base × height

= 1/2 × 8.9 × 6.8

= 60.52/2

Area of base = 30.26 cm

Volume of triangular prism = 1/3 × base area × height

= 1/3 × 30.26 × 7.2

= 217.87/3

= 72.6 cm³

Problem 9 :

Solution :

diameter = 18.2 m

Radius = 18.2/2 = 9.1 m

Height = 21.6 m

Base area = Area of circle

= πr²

= 22/7 × 9.1 × 9.1

= 260.26

Volume of cone = 1/3 × πr²h

= 1/3 × 260.26 × 21.6

V = 1873 m³