VERIFYING GEOMETRIC PROPERTIES OF QUADRILATERAL WITH ANALYTIC GEOMETRY
Proving it is Rectangle
To check of the given quadrilateral is a rectangle, we have to follow the procedure given below.
- In rectangle, the length of opposite sides will be equal.
- Each angle will be right angle.
- To prove this, by drawing a diagonal we can divide the rectangle into two right triangles.
- Using Pythagorean theorem, we can prove the triangle is a right triangle. Then, its angle measure is 90 degree.
Proving it is Parallelogram
To check of the given quadrilateral is a parallelogram, we have to follow the procedure given below.
- In parallelogram opposite sides are parallel and equal.
- Length of opposite sides will be equal.
- Slope of opposite side will be equal since they are parallel.
- Midpoint of the diagonals will be equal.
Proving it is Square
To check of the given quadrilateral is a square, we have to follow the procedure given below.
- In square the opposite sides are equal.
- Each angle measures will be 90 degree.
- By drawing the diagonal, we will get a right triangle.
- Using Pythagorean theorem, we can prove the angle measure is 90 degree.
Proving it is Rhombus
To check of the given quadrilateral is a rhombus, we have to follow the procedure given below.
- In rhombus, the diagonals will be perpendicular.
- If the product of slopes of diagonals is equal to -1, then the diagonals are perpendicular to each other.
Problem 1 :
Verify quadrilateral with vertices A(3, 4), B(1, 1), C(4, -4) and D(6, -1) is a parallelogram. To verify that the quadrilateral is a parallelogram, calculate
Solution :
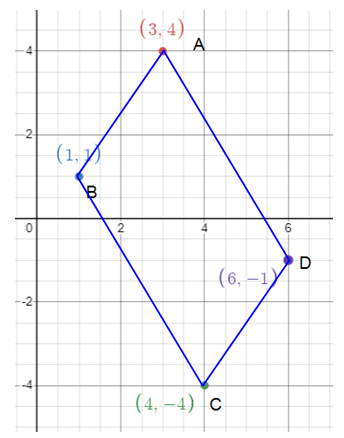
Given, A(3, 4), B(1, 1), C(4, -4) and D(6, -1)
D = √[(x2 - x1)2 + (y2 - y1)2]
Length of AB :
x1 = 3, y1 = 4, x2 = 1, y2 = 1
AB = √[(1 - 3)2 + (1 - 4)2]
= √[(-2)2 + (-3)2]
= √[4 + 9]
AB = √13 units
Length of BC :
B(1, 1), and C(4, -4)
x1 = 1, y1 = 1, x2 = 4, y2 = -4
BC = √[(4 - 1)2 + (-4 - 1)2]
= √[(3)2 + (-5)2]
= √[9 + 25]
BC = √34 units
Length of CD :
C(4, -4) and D(6, -1)
x1 = 4, y1 = -4, x2 = 6, y2 = -1
CD = √[(6 - 4)2 + (-1 + 4)2]
= √[(2)2 + (3)2]
= √[4 + 9]
CD = √13 units
Length of DA :
D(6, -1) and A(3, 4)
x1 = 6, y1 = -1, x2 = 3, y2 = 4
DA = √[(3 - 6)2 + (4 + 1)2]
= √[(-3)2 + (5)2]
= √[9 + 25]
DA = √34 units
Length of opposite sides are equal.
Slope of AB :
A(3, 4) and B = (1, 1)
x1 = 3, y1 = 4, x2 = 1, y2 = 1
Slope of BC :
B(1, 1), and C(4, -4)
x1 = 1, y1 = 1, x2 = 4, y2 = -4
Slope of CD :
C(4, -4) and D(6, -1)
x1 = 4, y1 = -4, x2 = 6, y2 = -1
Slope of DA :
D(6, -1) and A(3, 4)
x1 = 6, y1 = -1, x2 = 3, y2 = 4
The opposite sides AB, CD and BC, DA have the same slope and are thus parallel to each other.
The given quadrilateral ABCD is a parallelogram as the opposite sides are equal and parallel to each other.
Problem 2 :
Verify that quadrilateral DEFG is a square if D(5, 1), E(-1, 1), F(-1, -5) and G(5, -5).
Solution :
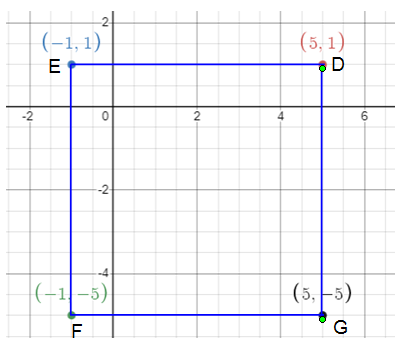
Given, D(5, 1), E(-1, 1), F(-1, -5) and G(5, -5)
Length of DE :
D(5, 1) and E(-1, 1)
x1 = 5, y1 = 1, x2 = -1, y2 = 1
DE = √[(-1 - 5)2 + (1 - 1)2]
= √[(-6)2 + (0)2]
DE = √36 units
Length of EF :
E(-1, 1) and F(-1, -5)
x1 = -1, y1 = 1, x2 = -1, y2 = -5
EF = √[(-1 + 1)2 + (-5 - 1)2]
= √[(0)2 + (-6)2]
EF = √36 units
Length of FG :
F(-1, -5) and G(5, -5)
x1 = -1, y1 = -5, x2 = 5, y2 = -5
FG = √[(5 + 1)2 + (-5 + 5)2]
= √[(6)2 + (0)2]
FG = √36 units
Length of GD :
G(5, -5) and D(5, 1)
x1 = 5, y1 = -5, x2 = 5, y2 = 1
GD = √[(5 - 5)2 + (1 + 5)2]
= √[(0)2 + (6)2]
GD = √36 units
DE = EF = FG = GD
Problem 3 :
A quadrilateral has vertices O(0, 0), P(3, 5), Q(8, 6) and R(5, 1). Verify that OPQR is a parallelogram.
Solution :
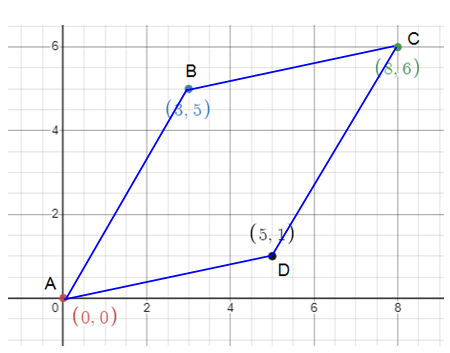
Given, O(0, 0), P(3, 5), Q(8, 6) and R(5, 1)
O(0, 0) and P(3, 5)
x1 = 0, y1 = 0, x2 = 3, y2 = 5
OP = √[(3 - 0)2 + (5 - 0)2]
= √[(3)2 + (5)2]
= √[9 + 25]
OP = √34 units
P(3, 5) and Q(8, 6)
x1 = 3, y1 = 5, x2 = 8, y2 = 6
PQ = √[(8 - 3)2 + (6 - 5)2]
= √[(5)2 + (1)2]
= √[25 + 1]
PQ = √26 units
Q(8, 6) and R(5, 1)
x1 = 8, y1 = 6, x2 = 5, y2 = 1
QR = √[(5 - 8)2 + (1 - 6)2]
= √[(-3)2 + (-5)2]
= √[9 + 25]
QR = √34 units
R(5, 1) and O(0, 0)
x1 = 5, y1 = 1, x2 = 0, y2 = 0
RO = √[(0 - 5)2 + (0 - 1)2]
= √[(-5)2 + (-1)2]
= √[25 + 1]
RO = √26 units
The opposite sides OP and QR are equal.
The opposite sides PQ and RQ are equal.
O(0, 0) and P(3, 5)
x1 = 0, y1 = 0, x2 = 3, y2 = 5
P(3, 5) and Q(8, 6)
x1 = 3, y1 = 5, x2 = 8, y2 = 6
Q(8, 6) and R(5, 1)
x1 = 8, y1 = 6, x2 = 5, y2 = 1
R(5, 1) and O(0, 0)
x1 = 5, y1 = 1, x2 = 0, y2 = 0
The opposite sides OP, QR and BC, DA have the same slope and are thus parallel to each other.
The given quadrilateral OPQR is a parallelogram as the opposite sides are equal and parallel.
Problem 4 :
Verify that the quadrilateral with vertices P(2, 3), Q(5, -1), R(10, -1) and S(7, 3) is a rhombus.
Solution :
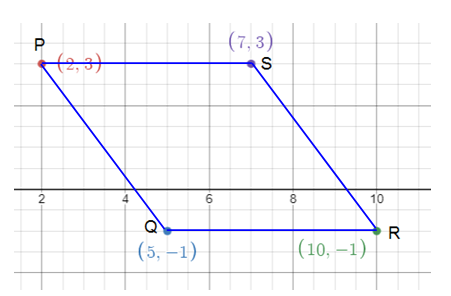
In rhombus, length of all sides will be equal and diagonals will be perpendicular to each other.
D = √[(x2 - x1)2 + (y2 - y1)2]
Length of PQ :
P(2, 3) and Q(5, -1)
PQ = √[(5 - 2)2 + (-1 - 3)2]
= √[(3)2 + (-4)2]
= √[9 + 16]
PQ = 5
Length of QR :
Q(5, -1) and R(10, -1)
QR = √[(10 - 5)2 + (-1 + 1)2]
= √[(5)2 + (0)2]
QR = 5
Length of RS :
R(10, -1) and S(7, 3)
RS = √[(7 - 10)2 + (3 + 1)2]
= √[(-3)2 + (4)2]
RS = √[9 + 16]
RS = 5
Length of SP :
S(7, 3) and P(2, 3)
SP = √[(2 - 7)2 + (3 - 3)2]
= √[(5)2 + (0)2]
SP = 5
PQ = QR = RS = SP. All sides are equal.
|
Slope of PR P(2, 3) and R(10, -1) m = (-1-3) / (10 - 2) = -4/8 = -1/2 |
Slope of SQ S(7, 3) and Q(5, -1) m = (-1-3) / (5 -7) = -4/-2 = 2 |
Slope of PR x Slope of SQ = (-1/2) x 2
= -1
So, the required quadrilateral will be a rhombus.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling