USING REFERENCE ANGLES TO FIND TRIG VALUES

Let A be an angle in standard position. The reference angle B associated with A is the acute angle formed by the terminal side of A and the x-axis.

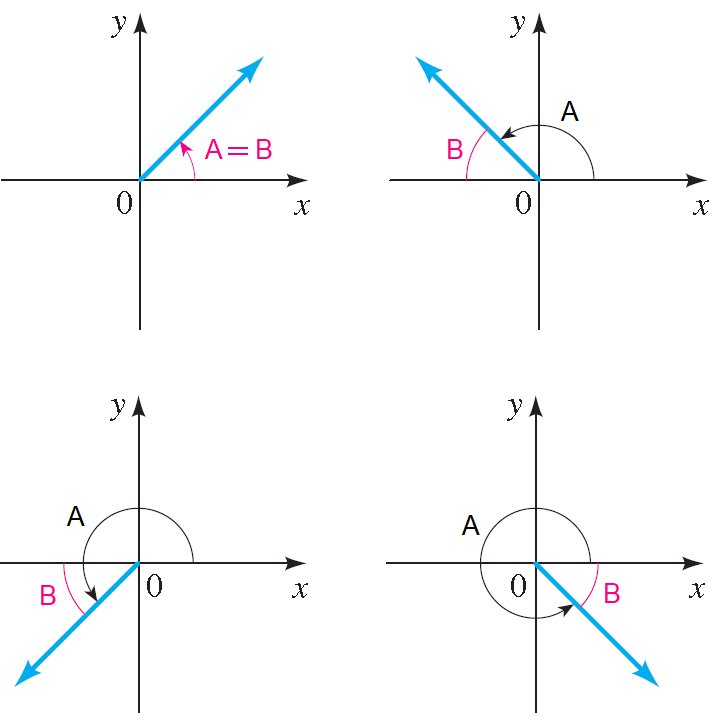
Ensure that the given angle is positive and it is between 0° and 360°.

What if the given angle does not meet the criteria above :

Let θ be the angle given.

Problem 1 :

Solution:

Problem 2 :

Solution:

Problem 3 :

csc 240°

Solution:

Since the angle lies in 3rd quadrant, using ASTC we use negative sign.

θ = 240°

Reference angle = θ - 180

= 240 - 180

= 60

csc 240° = - csc 60°

= -2/√3

Problem 4 :

sec -330°

Solution:

θ = 330

Since the angle lies in 4^th quadrant, using ASTC we use positive sign.

Reference angle = 360 - θ 

= 360 - 330

= 30

sec -330° = sec 30°

Problem 5 :

sin 120°

Solution:

θ = 120

Since the angle lies in 2nd quadrant, using ASTC we use positive sign.

Reference angle = 180 - θ 

= 180 - 120

= 60

sin 120° = sin 60°

= √3/2

Problem 6 :

csc -240°

Solution:

θ = 240

Since the angle lies in 3rd quadrant, using ASTC we use negative sign.

Reference angle = θ - 180 

= 240 - 180

= 60

csc -240° = - csc 60°

= -2/√3

Problem 7 :

tan 240°

Solution:

θ = 240

Since the angle lies in 3rd quadrant, using ASTC we use positive sign.

Reference angle = θ - 180

= 240 - 180

= 60

tan 240° = tan 60°

= √3

Problem 8 :

cos -210°

Solution:

θ = 210

Since the angle lies in 3rd quadrant, using ASTC we use negative sign.

Reference angle = θ - 180

= 210 - 180

= 30

cos -210° = - cos 30°

= -√3/2

Problem 9 :

cot 0°

Solution:

cot 0° = undefined

Problem 10 :

Solution:

Here θ lies in 4th quadrant. Using ASTC, we use negative sign.

Reference angle = 2π - θ

Problem 11 :

sec 210°

Solution:

θ = 210

Since the angle lies in 3rd quadrant, using ASTC we use negative sign.

Reference angle = θ - 180

= 210 - 180

= 30

sec 210° = -sec 30°

Problem 12 :

cot -150°

Solution:

θ = 150

Since the angle lies in 2nd quadrant, using ASTC we use negative sign.

Reference angle = 180 - θ 

= 180 - 150

= 30

cot 210° = -cot 30°

= -√3

Problem 13 :

sin -60°

Solution:

θ = 60

Since the angle lies in 1st quadrant, using ASTC we use positive sign.

Reference angle = θ 

sin -60° = sin 60

= √3/2

Problem 14 :

sec 45°

Solution:

θ = 45

Since the angle lies in 1st quadrant, using ASTC we use positive sign.

Reference angle = θ 

sec 45° = sec 45°

= √2

Problem 15 :

cos 180°

Solution:

θ = 180

Since the angle lies in 2nd quadrant, using ASTC we use negative sign.

Reference angle = 180 - θ 

= 180 - 180

= 0

cos 180° = -cos 0°

= -1

Problem 16 :

Solution:

Problem 17 :

Solution:

Problem 18 :

Solution:

Problem 19 :

Solution:

Problem 20 :

Solution: