USING HERONS FORMULA FIND THE AREA

A scalene triangle is a triangle in which all three sides are in different lengths, and all three angles are of different measures.

For example,

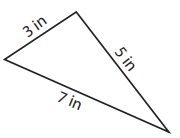
All measures are different, so it is scalene triangle.

To find area of scalene triangle, we use the formula

Area of triangle - √ (s(s - a) (s - b) (s - c))

Here a, b and c are sides of the triangle.

s = (a + b + c)/2

Problem 1 :

Find the area of the right angled triangle with sides 3 cm, 4 cm and 5 cm:

i) Without using Heron's formula     ii) Using Heron's formula

Solution:

i) Without using Heron's formula:

3 cm, 4 cm, and 5 cm

3²+ 4² = 5²

9 + 16 = 25

L.H.S = R.H.S

This is a right angled triangle.

Area of triangle = 1/2 × b × h

= 1/2 × 3 × 4

A = 6 cm²

ii) Using Heron's formula:

Area of triangle = √ (s(s - a) (s - b) (s - c))

s = (a + b + c) / 2

= (3 + 4 + 5) / 2

= 12/2

s = 6 cm

A = √ (s(s - a) (s - b) (s - c))

= √ (6(6 - 3) (6 - 4) (6 - 5))

= √ (6 × 3 × 2 × 1)

= √36

A = 6 cm²

Problem 2 :

Find the area of a triangle with sides of length:

i) 6 cm, 8 cm and 12 cm

Solution:

Area of triangle - √ (s(s - a) (s - b) (s - c))

s = (a + b + c) / 2

= (6 + 8 + 12) / 2

= 26/2

s = 13 cm

A = √ (13(13 - 6) (13 - 8) (13 - 12))

= √ (13 × 7 × 5 × 1)

= √455

A = 21.3 cm²

ii) 7.2 cm, 8.9 cm and 9.7 cm

Solution:

Area of triangle - √ (s(s - a) (s - b) (s - c))

s = (a + b + c) / 2

= (7.2 + 8.9 + 9.7) / 2

= 25.8/2

s = 12.9 cm

A = √ (12.9)(12.9 - 7.2) (12.9 - 8.9) (12.9 - 9.7))

= √ (12.9)(5.7) (4) (3.2)

= √ 941.184

A = 30.7 cm²

Problem 3 :

Find the area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm.

Solution:

s = (a + b + c) / 2

 = (4 + 4 + 2) / 2 

s = 10/2

s = 5

Area of the triangle = √ (s(s - a) (s - b) (s - c))

= √ (5(5 - 4) (5 - 4) (5 - 2))

= √5(1)(1)(3)

= √15 cm²

So, area of an isosceles is √15 cm².

Problem 4 :

How many times area is changed, when sides of a triangle are doubled.

Solution:

Let the base of the original triangle be a units and height be b units.

The area of original triangle = (1/2) ab

Each side of a triangle is doubled.

Thus, base of the new triangle is 2a units and height is 2b units.

Area of new triangle = (1/2) × 2a × 2b

= 1/2 × 4ab

= 4 × (1/2) ab

= 4 × area of original triangle

Hence, if each side of a triangle is doubled, then its area is 4 times the area of the original triangle.

Problem 5 :

If the perimeter of an isosceles triangle is 11 cm and its base is 5 cm, its area is 5/4 √11 cm². State true or false and give reason. 

Solution:

P = x + x + 5 = 11 cm

2x + 5 = 11 

2x = 6

x = 3 cm

Area = (1/2) × base × height

h = √ (3² - (5/2)²) 

= √ (9 - 25/4)

= √ (11/4)

Area = (1/2) × √11/4 × 5

= 5/4 √11 cm²

Hence, the statement is true.

Problem 6 :

The cost of levelling a ground in the form of a triangle having the sides 51 m, 71 m, and 20 m at the rate of '3 per m² is '918. State whether the statement is true or false and justify your answer.

Solution:

s = (a + b + c) / 2

= (51 + 71 + 20) / 2

= 108 / 2

s = 54

Area of the triangle = √ (s(s - a) (s - b) (s - c))

= √ (54(54 - 51) (54 - 37) (54 - 20))

= √ 54(3)(17)(34)

= √ 93636

Area = 306 m².

Cost of levelling at '3 per m² = 306(3)

= '918

Hence, the statement is true.

Problem 7 :

The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3: 2. Find the area of the triangle.

Solution:

Given, perimeter of triangle = 32 cm

Let the sides be 3x, 2x. Let the third side = 3x

perimeter = 3x + 3x + 2x 

3x + 3x + 2x = 32

8x = 32

x = 4 

Thus, the sides are 12 cm, 8 cm, 12 cm.

s = (a + b + c) / 2

= (12 + 8 + 12) / 2

= 32/2 

s = 16 cm

Area of the triangle = √ (s(s - a) (s - b) (s - c))

= √(16(16 - 12) (16 - 8) (16 - 12))

= √(16 × 4 × 8 × 4)

= √2048

= 32√2 cm²

So, area of an isosceles triangle is 32√2 cm².

Problem 8 :

The lengths of the sides of a triangle are 7 cm, 13 cm and 12 cm. Find the length of perpendicular from the opposite vertex to the side whose length is 12 cm.

Solution:

Sides of a triangle are 7 cm, 13 cm, 12 cm

s = (a + b + c) / 2

s = (7 + 13 + 12) / 2

= 32/2

s = 16 cm

Area of the triangle = √ (s(s - a) (s - b) (s - c))

= √(16(16 - 7) (16 - 13) (16 - 12))

= √(16 × 9 × 3 × 4)

= √1728

= 12√12

There is perpendicular from the opposite vertex to the side 12 cm.

1/2 × b × h = 12√12

1/2 × 12 × h = 12√12

h = 2√12

h = 2 × 2√3

h = 4√3 cm

Hence, the length of perpendicular is 4√3 cm.