USING EQUATIONS FINDING THE LENGTH OF THE LINE SEGMENT

In the diagram given below, M is the midpoint of the segment. Find the indicated length.

Problem 1 :

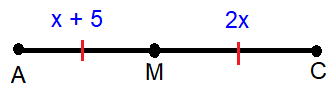
Find length of AM.

Solution :

In the given diagram,

M is the midpoint of AC.

AM = x + 5, MC = 2x

x + 5 = 2x

 5 = 2x – x

5 = x

x = 5 substitute in AM = x + 5

AM = 5 + 5

AM = 10

So, the value of AM is 10.

Problem 2 :

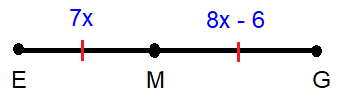
Find the length of EM

Solution :

In the given diagram,

M is the midpoint of EG.

EM = 7x, MG = 8x - 6

7x = 8x - 6

 7x – 8x = – 6

-x = -6

x = 6

x = 6 Substitute in EM = 7x

EM = 7(6)

EM = 42

So, the length of EM is 42.

Problem 3 :

Solution :

In the given diagram,

M is the midpoint of JM.

JM = 6x + 7, ML = 4x + 5

6x + 7 = 4x + 5

 6x - 4x = 5 - 7

2x = -2

x = -1

x = -1 Substitute in JM = 6x + 7

JM = 6(-1) + 7

JM = -6 + 7

JM = 1

So, the value of JM is 1.

Problem 4 :

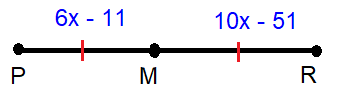
Find the length of PR.

Solution :

In the given diagram,

M is the midpoint of PR.

PM = 6x - 11, MR = 10x – 51

PM = MR

6x - 11 = 10x - 51

 6x – 10x = – 51 + 11

-4x = -40

x = 10

MR = 10x – 51

= 10(10) – 51

= 100 – 51

MR = 49

PM = 10

PR = 49 + 10

PR = 59

So, the length of PR is 59.

Problem 5 :

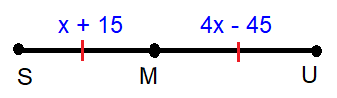
Find SU.

Solution :

In the given diagram,

M is the midpoint of SU.

SM = x + 15, MU = 4x – 45

SM = MU

x + 15 = 4x - 45

 x – 4x = – 45 - 15

-3x = -60

x = 60/3

x = 20

MU = 4x – 45

= 4(20) – 45

= 80 – 45

MU = 35

SM = 10

SU = 35 + 10

SU = 45

So, the value of SU is 45.

Problem 6 :

Find XZ.

Solution :

In the given diagram,

M is the midpoint of XZ.

XM = 2x + 35, MZ = 5x – 22

XM = MZ

2x + 35 = 5x - 22

 2x – 5x = – 22 - 35

-3x = -57

x = 57/3

x = 19

MZ = 5x – 22

= 5(19) – 22

= 95 – 22

MZ = 73

XM = 19

XZ = 73 + 19

XZ = 92

So, the length of XZ is 92.

Problem 7 :

Point M is the midpoint of VW. Find the length of VM.

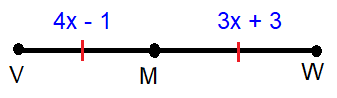
Solution :

In the given diagram,

M is the midpoint of VW.

VM = 4x - 1, MW = 3x + 3

4x - 1 = 3x + 3

 4x – 3x = 3 + 1

x = 4

x = 4 substitute in VM = 4x - 1

VM = 4(4) - 1

VM = 15

So, the length of VM is 15. 

Problem 8 :

The straight line l has a gradient of 5/12, and passes through the points A(10, 1) and B(k, 11), where k is a constant.

a)  Find an equation of l, in the form ax + by = c, where a, b and c are integers.

b) Determine the value of k.

c) Hence show that the distance AB is 26 units.

Solution :

Slope = 5/12

a)  Equation of the line which has the slope 5/12 and passes through the point A(10, 1).

(y - y₁) = m(x -x₁)

(y - 1) = 5/12(x - 1)

12(y - 1) = 5(x - 1)

12y - 12 = 5x - 5

5x - 12y - 5 + 12 = 0

5x - 12y + 7 = 0

b)

Slope of the line joining the points = (y₂ - y₁) / (x₂  - x₁)

5/12 = (11 - 1) / (k - 10)

5/12 = 10/(k - 10)

5(k - 10) = 10(12)

5k - 50 = 120

5k = 120 + 50

5k = 170

k = 170/5

k = 34

c)   A(10, 1) and B(34, 11)

Distance between the points = √(x₂ - x₁)² + (y₂ - y₁)²

= √(11-1)² + (34-10)²

= √10² + 24²

= √100 + 576

= √676

= 26 units

The straight line l₁ passes through the points A(1, -1) and B(7, 8)

a) Find the equation of l₁

b) Show that the length of AB is k√13, where k is the integer.

Solution :

A(1, -1) and B(7, 8)

a) Slope of the line passes through the points = (8 - (-1)) / (7 - 1)

= (8 + 1)/6

= 9/6

= 3/2

Equation of hte line :

(y - (-1)) = 3/2(x - 1)

2(y + 1) = 3(x - 1)

2y + 2 = 3x - 3

3x - 2y - 3 - 2 = 0

3x - 2y - 5 = 0

b)  A(1, -1) and B(7, 8)

Distance between the points = √(x₂ - x₁)² + (y₂ - y₁)²

= √(8 + 1)² + (7 - 1)²

= √9² + 6²

= √(81 + 36)

= √117

= √(3 x 3 x 13)

= 3√13

Comapring with k√13, the value of k is 3.