USING CHAIN RULE TO FIND DERIVATIVE

In differential calculus, the chain rule is a formula used to find the derivative of a composite function.

If y = f(g(x)), then as per chain rule the instantaneous rate of change of function 'f' relative to 'g' and 'g' relative to x results in an instantaneous rate of change of 'f' with respect to 'x'.

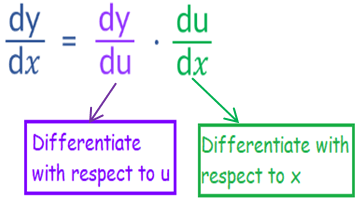
Use the chain rule to find dy/dx at the indicated value of x.

Problem 1 :

y = 2u² + 5 and u = 3x, when x = 1

Solution :

y = 2u² + 5 and u = 3x

Here y is defined in terms of u and u is defined in terms of x.

(1) ⋅ (2)

dy/dx = (dy/du) ⋅ (du/dx)

 = 4u ⋅ 3

= 12 u

Here u = 3x

dy/dx = 12(3x)

dy/dx = 36x

dy/dx at x = 1 ==> 36(1) = 36

Problem 2 :

y = u² - 5u and u = 2x + 1, when x = 0

Solution :

y = u² - 5u and u = 2x + 1

Here y is defined in terms of u and u is defined in terms of x.

(1) ⋅ (2)

dy/dx = (dy/du) ⋅ (du/dx)

 = (2u - 5) ⋅ 2

= 4u - 10

Here u = 2x - 1

dy/dx = 4(2x-1) - 10

= 8x - 4 - 10

= 8x - 14

dy/dx = 8x - 14

dy/dx at x = 0 ==> 8(0) - 14 ==> -14

Problem 3 :

y = 5/(u + 2) and u = 3x - 2, when x = 1

Solution :

y = 5/(u + 2) and u = 3x - 2

Here y is defined in terms of u and u is defined in terms of x.

y = 5(u + 2)^-1

(1) ⋅ (2)

dy/dx = (dy/du) ⋅ (du/dx)

 = -5/(u+2)² ⋅ 3

dy/dx = -15/(u + 2)²

Here u = 3x - 1

dy/dx = -15/(3x - 1 + 2)²

= -15/(3x + 1)²

When x = 1

dy/dx = -15/(3(1) + 1)²

dy/dx = -15/16

Problem 4 :

y = √(u² + 3) and u = 2x² - 1, when x = 1

Solution :

y = √(u² + 3) and u = 2x² - 1

Here y is defined in terms of u and u is defined in terms of x.

Problem 5 :

Solution :

Multiplying (1) and (2), we get