USE RATIOS TO DETERMINE WHETHER THE TRIANGLES ARE SIMILAR

State if the triangles in each pair are similar. If so, state how you know they are similar and complete the similarity statement.

Problem 1 :

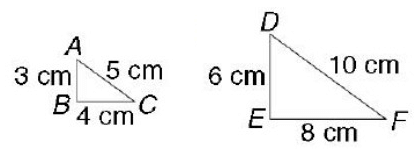
Solution :

By observing the figure,

AB : DE = 3 : 6 = 3/6 = 1/2

BC : EF = 4 : 8 = 4/8 = 1/2

CA = FD = 5 : 10 = 5/10 = 1/2

So, the triangles are similar. Using the postulate SSS.

Problem 2 :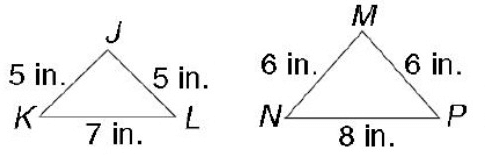

Solution :

By observing the figure,

KL : NP = 7 : 8 = 7/8

KJ : NM = 5 : 6 = 5/6

JL = MP = 5 : 6 = 5/6

So, the triangles are not similar. Using the postulate SSS.

Problem 3 :

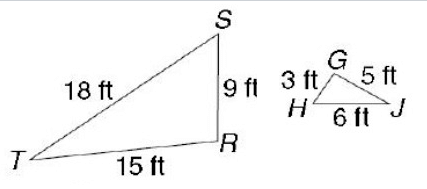
Solution :

By observing the figure,

ST : HJ = 18 : 6 = 18/6 = 3

TR : JG = 15 : 5 = 15/5 = 3

SR : GH = 9 : 3 = 9/3 = 3

So, the triangles are similar. Using the postulate SSS.

Problem 4 :

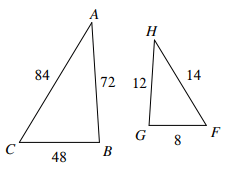
Solution :

AC / HF = 84/14 ==>  6

AB / HG = 72/12 ==> 6

BC / GF = 48/8 ==> 6

The triangles are similar. Using the postulate SSS.

Find the missing length. The triangles in each pair are similar.

Problem 5 :

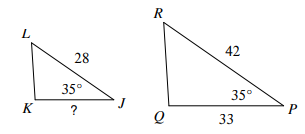
Solution :

From the figure above LJ and RP are similar sides.

The ratio,

LJ / RP ==> 28/42 ==>  2/3

So, KJ and QP are corresponding sides.

KJ/QP = 2/3

KJ/33 = 2/3

KJ = (2/3)(33)

KJ = 22

Problem 6 :

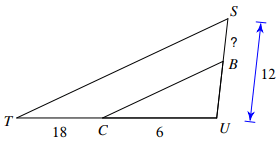
Solution :

Here triangles CUB and TSU are similar,

Let BU = x, SB = 12 - x

Corresponding sides are

BU is similar to SU.

CU is similar to TU.

BC is similar to ST.

BU/SU = CU/TU

x/12 = 6/(18+6)

x/12 = 6/24

x = (1/4)(12)

x = 3

Then, SB = 12 - 3 ==> 9

Tell whether the triangles are similar. Explain.

Problem 7 :

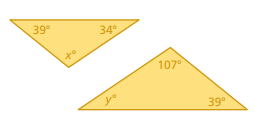
Solution :

In the above triangles, we have 39 as common. The base angles are 39 and 34. Then, y = 34 and x = 34

Problem 8 :

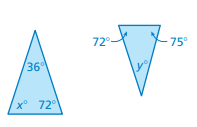
Solution :

The base angles are 72 and 75.

x = 75 and y = 36.

Problem 9 :

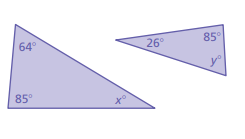
Solution :

Two of the angles are 85 and 64 in the first triangle. Then y = 64.