USE PROPERTIES OF QUADRILATERALS TO SOLVE PROBLEMS

Problem 1 :

Use the parallelogram given below.

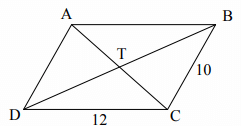
1. Find the perimeter.

2. If CT = 9, find AT.

3. If m∠CDA = 60° , find m∠CBA and m∠BAD .

4. If AT = 4x – 7 and CT = –x + 13 , solve for x.

Solution :

1) Perimeter of parallelogram ABCD = AB + BC + CD + DC

= 12 + 10 + 12 + 10

= 42

2)  CT = 9

In parallelogram, the diagonals will be perpendicular and bisect each other.

So, AT = 9

3. If m∠CDA = 60° , find m∠CBA and m∠BAD .

In parallelogram, opposite angles are equal. ∠CBA = 60

∠CBA + ∠BAD = 180 (co-interior angles)

60 + ∠BAD = 180

∠BAD = 180 - 60

∠BAD = 120

4. If AT = 4x – 7 and CT = –x + 13 , solve for x.

AT = CT (diagonals will bisect each other)

4x - 7 = -x + 13

4x + x = 13 + 7

5x = 20

x = 4

Problem 2 :

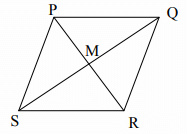
For problems 5-8 use the rhombus below.

5. If PS = 6 , what is the perimeter of PQRS?

6. If PQ = 3x + 7 and QR = –x + 17, solve for x.

7. If m∠PSM = 22° , find m∠RSM and m∠SPQ .

8. If m∠PMQ = 4x – 5, solve for x.

Solution :

5)  In rhombus, all sides will be equal.

Perimeter of rhombus = 4(6) ==> 24

6)  PQ = QR

3x + 7 = -x + 17

3x + x = 17 - 7

4x = 10

x = 2.5

7. If m∠PSM = 22° , find m∠RSM and m∠SPQ .

m∠PSM = 22° = m∠RSM

m∠SPM =  m∠MPQ

In triangle SPQ,

m∠PSM + m∠SPM + m∠MPQ + m∠RSM = 180

22 + 2∠SPM + 22 = 180

2∠SPM = 180 - 44

2∠SPM = 136

∠SPM = 136/2

∠SPM = 68

∠SPQ = m∠SPM + m∠MPQ

= 68 + 68

∠SPQ = 136

8. If m∠PMQ = 4x – 5, solve for x.

In rhombus, the diagonals will be perpendicular.

4x - 5 = 90

4x = 95

x = 95/4

x = 23.75

Problem 3 :

For problems 9-12 use the quadrilateral at right.

9. If WX = YZ and WZ = XY, must WXYZ be a rectangle?

10. If m∠WZY = 90° , must WXYZ be a rectangle?

11. If the information in problems 9-10 are both true, must WXYZ be a rectangle?

12. If WY = 15 and WZ = 9, what is YZ and XZ?

Solution :

In rectangle, opposite sides will be equal and each vertex we will have 90 degree.

9. If WX = YZ and WZ = XY, must WXYZ be a rectangle?

From the given, the opposite sides are equal, it may be a parallelogram also. 

10. If m∠WZY = 90° , must WXYZ be a rectangle?

If m∠WZY = 90°, then m∠ZYX = 90° (co-interior angles)

11. If the information in problems 9-10 are both true, then it must WXYZ be a rectangle

12. Given WY = 15

WY is a diagonal of the rectangle.

(WY)² = (WZ)² + (ZY)²

15² = 9² + (ZY)²

225 - 81 = (ZY)²

(ZY)² = 144

ZY = 12

XZ is opposite to ZY. Then XZ = 12.

Problem 4 :

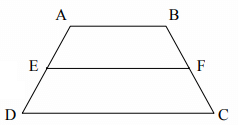
For problems 13-16 use the trapezoid at right with midpoints E and F.

13. If m∠EDC = 60° , find m∠AEF .

14. If m∠DCB = 5x + 20 and m∠ABC = 3x + 10, solve for x.

15. If AB = 6 and DC = 10, find EF.

16. If EF = 9 and DC = 15, find AB.

Solution :

13. AB, EF and DC are parallel.

m∠EDC = 60° = m∠AEF = 60°

14. m∠DCB = 5x + 20 -----(1)

m∠ABC = 3x + 10 -----(2)

(1) = (2)

5x + 20 = 3x + 10

5x - 3x = 10 - 20

2x = -10

x = -5

15. If AB = 6 and DC = 10, find EF.

Problem 5 :

For problems 17-20 use the kite given below.

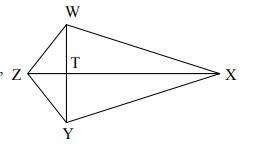
17. If m∠XWZ = 95° , find m∠XYZ.

18. If WZ = 5 and WT = 4, find ZT.

19. If WT = 4, TZ = 3, and TX = 10, find the perimeter of WXYZ.

Solution :

17. m∠XWZ = 95° = m∠XYZ.

18.  In triangle ZWX.

m∠WXY = 40°/2

m∠WXT = 20

∠WZT + ∠WXT + ∠ZWX = 180

110 + 20 + ∠ZWX = 180

∠ZWX = 180 - 130

∠ZWX = 50

19. If WZ = 5 and WT = 4, find ZT.

In triangle WZT.

WY and ZX are perpendicular.

(ZT)² + (TW)² = (ZW)²

(ZT)² + 4² = 5²

(ZT)² = 25 - 16

(ZT)² = 9

ZT = 3

20. If WT = 4, TZ = 3, and TX = 10, find the perimeter of WXYZ.

In triangle WZT

(ZT)² + (TW)² = (ZW)²

3² + 4² = (ZW)²

9 + 16 = (ZW)²

(ZW)² = 25

ZW = 5

In triangle WTX

(WT)² + (TX)² = (WX)²

4² + 10² = (WX)²

16 + 100 = (WX)²

(WX)² = 116

WX = √116

Perimeter = ZW + WX + XY + ZY

= 2(ZW) + 2(WX)

= 2(5) + 2√116

= 10 + 2√116