USE GEOMETRIC FORMULA TO EVALUATE THE INTEGRAL
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
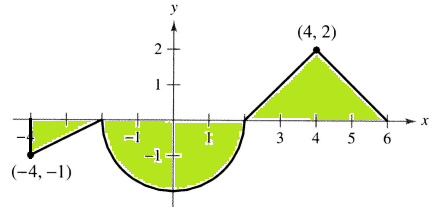
The graph of f consists of line segments and a semicircle, as shown. Evaluate each definite integral by using geometric formulas.
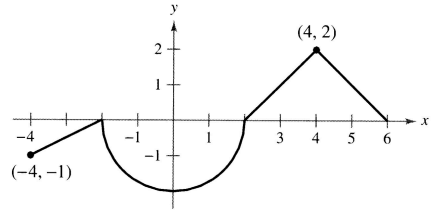
Problem 1 :
Solution :
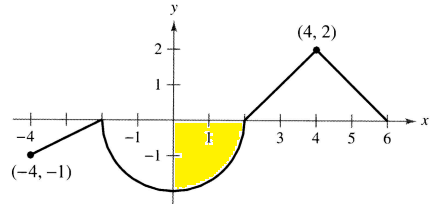
The shaded region is a quadrant. The geometric formula to find area of quadrant is (1/4) πr2
The required area is below the x-axis, it should be negative.
radius = 2 units
Area of quadrant = (1/4) πr2
= (1/4) π(2)2
= -π
Problem 2 :
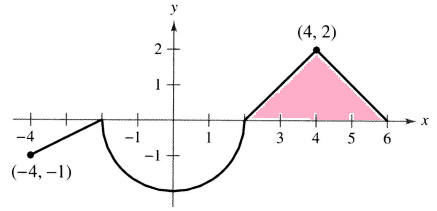
From the given integral, we understand that the required area is triangle. The shaded region is above the x-axis, it should be positive.
Area of triangle = (1/2) x base x height
base = 4 units and height = 2 units
= (1/2) x 4 x 2
= 4
Problem 3 :
Solution :
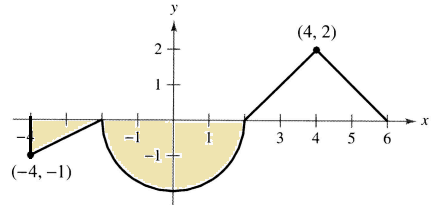
From the given definite integral, we understand that the required area will be sum of area of triangle and area of semicircle.
The required region is below the x-axis, so it should be negative.
Area of triangle = (1/2) x base x height
base = 2 and height = 1
= (1/2) x 2 x 1
= 1 ------(1)
Area of semicircle = (1/2) x πr2
radius = 2 units
= (1/2) x π(2)2
= 2π ----(2)
(1) + (2)
= -(1 + 2π)
Problem 4 :
Solution :
Problem 5 :
Solution :
Problem 6 :
Solution :
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling