USE FIRST DERIVATIVE TEST TO FIND EXTREMA

Find the following :

(a) find the critical numbers of f, if any,

(b) find the open intervals on which the function is increasing or decreasing,

(c) apply the First Derivative Test to identify all relative extrema, and

(d) use a graphing utility to confirm your results.

Problem 1 :

f(x) = x² − 8x

Solution :

f(x) = x² − 8x

f'(x) = 2x - 8

f'(x) =  2(x - 4)

f'(x) = 0

2(x - 4) = 0

x = 4

Critical number is at x = 4

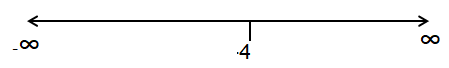
Intervals are (-∞, 4) and (4, ∞)

• In the interval (-∞, 4), we have negative slope. So, it is decreasing in the interval (-∞, 4).
• In the interval (4, ∞), we have positive slope. So, it is increasing in the interval (4, ∞).

Negative --> Positive --> Relative minimum

Relative minimum at x = 4

f(4) = 4² − 8(4)

f(4) = 16 − 32

f(4) = -16

Relative minimum is (4, -16)

Problem 2 :

f(x) = -2x² + 4x + 3

Solution :

f(x) = -2x² + 4x + 3

f'(x) = -4x + 4

f'(x) =  -4(x - 1)

f'(x) = 0

-4(x - 1) = 0

x = 1

Critical number is at x = 1

Intervals are (-∞, 1) and (1, ∞)

• In the interval (-∞, 1), we have positive slope. So, it is increasing in the interval (-∞, 1).
• In the interval (1, ∞), we have negative slope. So, it is decreasing in the interval (1, ∞).

Positive --> Negative --> Relative maximum

Relative maximum x = 1

f(1) = -2(1)² + 4(1) + 3

f(1) = -2 + 4 + 3

f(1) = -2 + 7

f(1) = 5

Relative maximum is (1, 5)

Problem 3 :

f(x) = -7x³ + 21x + 3

Solution :

f(x) = -7x³ + 21x + 3

f'(x) = -21x² + 21

f'(x) = -21(x² - 1)

f'(x) = 0

-21(x² - 1) = 0

x² - 1 = 0

x = ±1

Critical number is at x = -1 and 1

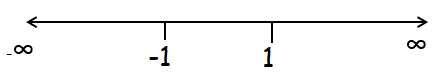
Intervals are (-∞, -1), (-1, 1) and (1, ∞)

• In the interval  (-∞, -1), we have negative slope. So, it is decreasing in the interval (-∞, -1).
• In the interval (-1, 1), we have positive slope. So, it is increasing in the interval (-1, 1).
• In the interval  (1, ∞), we have negative slope. So, it is decreasing in the interval (1, ∞).

Negative --> Positive --> Relative minimum

Positive --> Negative --> Relative maximum

Relative minimum at x = -1

f(-1) = -7(-1)³ + 21(-1) + 3

f(-1) = -7 - 21 + 3

f(-1) = -28 + 7

f(-1) = -21

Relative minimum is (-1, -21)

Relative maximum at x = 1

f(1) = -7(1)³ + 21(1) + 3

f(1) = -7 + 21 + 3

f(1) = -7 + 24

f(1) = 17

Relative maximum is (1, 17)

Problem 4 :

f(x) = (x - 1)²(x + 3)

Solution :

f(x) = (x - 1)²(x + 3)

Using product rule, finding the derivative. we get

u = (x - 1)² and  v = (x + 3)

u' = 2(x - 1)  and v' = 1

f'(x) = (x - 1)²(1) + 2(x - 1)(x + 3)

f'(x) = x²- 2x + 1 + 2(x² + 2x - 3)

f'(x) = x²- 2x + 1 + 2x² + 4x - 6

f'(x) = 3x² + 2x - 5

f'(x) = 3x² + 2x - 5 = 0

(3x + 5)(x - 1) = 0

x = -5/3 and x = 1

(-∞, -5/3), (-5/3, 1) and (1, ∞)

• In the interval (-∞, -5/3), we have positive slope. So, it is increasing in the interval (-∞, -5/3).
• In the interval  (-5/3, 1), we have negative slope. So, it is decreasing in the interval  (-5/3, 1).
• In the interval (1, ∞), we have positive slope. So, it is increasing in the interval  (1, ∞).

Positive --> Negative --> Relative maximum

Negative --> Positive --> Relative minimum 

Relative maximum at x = -5/3

f(-5/3) = (-5/3 - 1)²(-5/3 + 3)

f(-5/3) = (64/9) (4/3)

f(-5/3) = 256/27

Relative minimum is (-5/3, 256/27)

Relative maximum at x = 1

f(1) = (1 - 1)²(1 + 3)

f(1) = 0

Relative minimum is (1, 0)