TYPES OF SOLUTIONS SYSTEM OF EQUATIONS

The value that satisfies the equation is known as solution. When we have systems of equations, there are three types of solutions.

i)  Unique solution

ii)  Infinitely many solutions

iii) No solution

Unique Solution

The following lines are intersecting at a point, then the point of intersection is known as solution.

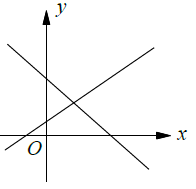
Infinitely Many Solution

The above lines are meeting at infinitely many points. The lines which are having infinitely many solutions,

The lines will have equal slopes and equal y-intercepts.

No Solution

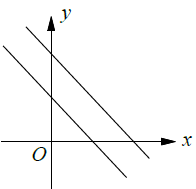
The above lines are parallel, they will never meet. So, no point of intersection and no solution.

Slopes will be equal, y-intercepts will not be equal.

Decide if the following systems of equations have a single solution, no solutions, or infinite solutions. If it has a solution, solve the system.

Problem 1 :

x + y = 1

x + y = 5

Solution :

Converting both equations into slope intercept form, we get

Slopes are same and y-intercepts are different. So, the lines are parallel.

Hence, the system has no solution.

Problem 2 :

2x + 3y = 7

4x + 5y = 13

Solution :

Converting the given equations into slope intercept form, we get

Slopes are different and y-intercept are also different.

In the given two linear equations, the slopes are different.

The system has one solution.

2x + 3y = 7 ---> (1)

4x + 5y = 13 ---> (2)

(1) ⋅ 2 - (2) 

(4x + 6y) - (4x + 5y) = 14 - 13

6y - 5y = 1

y = 1

By applying y = 1 in equation (1)

2x + 3(1) = 7

2x + 3 = 7

2x = 7 - 3

2x = 4

x = 2

Hence, the solution is x = 2 and y = 1.

Problem 3 :

1/2x + 3y = 1

x + 6y = 2

Solution :

(1/2)x + 3y = 1

x + 6y = 2

Converting the given equations into slope intercept form, we get

Since slope and y-intercepts are equal, it will have infinitely many solution. 

Problem 4 :

x + (1/3)y = -10

3x + y = 30

Solution :

Slopes are equal and y-intercepts are not equal. So, the lines are parallel. Then, the system has no solution.

Problem 5 :

2y = 6

3(x + y) = 12

Solution :

Converting the given equations into slope intercept form, we get

Slopes and y-intercepts are not equal, then there will be unique solution.

y = 3

By applying the value of y in 3x + 3y = 12, we get

3x + 3(3) = 12

3x + 9 = 12

3x = 12 - 9

3x = 3

x = 1

Hence, the solution are x = 1 and y = 3.

Problem 6 :

x + y = 2

3x + 3y = 6

Solution :

Converting the above equations into slope intercept form, we get

Slopes are equal, y-intercepts are also equal. So, the system has infinitely many solution.