TRANSLATIONS ON PARENT FUNCTIONS

There are types of transformations, they are

1) translation

2) reflection

3) stretch or shrink

Here translation means, moving the curve horizontally towards right or left.

Using parent function, we can the get the graph of any function using the concept of transformations.

Problems on Translation of Parent Functions

Give the name of the parent function and describe the transformation represented. You may use your graphing calculator to compare & sketch.

Problem 1 :

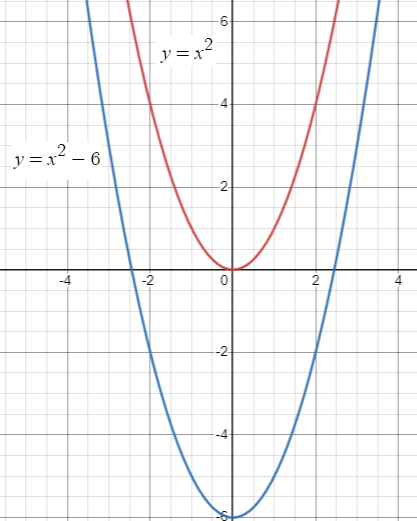
g(x) = x² - 6

Solution :

By observing the function g(x), the highest exponent is 2. So, it must be the quadratic function. 

Parent function :

f(x) = x²

Transformation :

Comparing with the parent function, k = -6, then we can move the graph 6 units down.

Problem 2 :

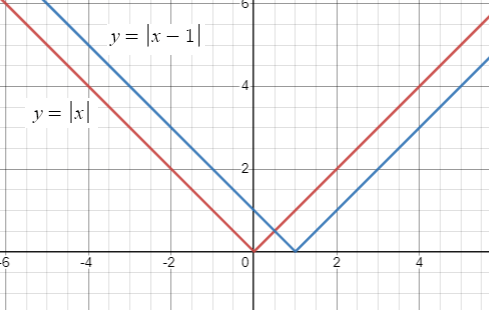
g(x) = |x - 1|

Solution :

By observing the function g(x), the highest exponent of x is 1 and it is inside the absolute sign. So, its graphical form will be in the shape of V. 

Parent function :

f(x) = |x|

Transformation :

Comparing with the parent function, in the function g(x) h = 1, the graph should be moved towards right 1 unit.

Problem 3 :

g(x) =  √x+4

Solution :

By observing the function g(x), we have square root sign. So, it is square root function.

Parent function :

f(x) = √x

Transformation :

Comparing with the parent function, in the function g(x) k = 4, the graph should be moved towards up 4 units.

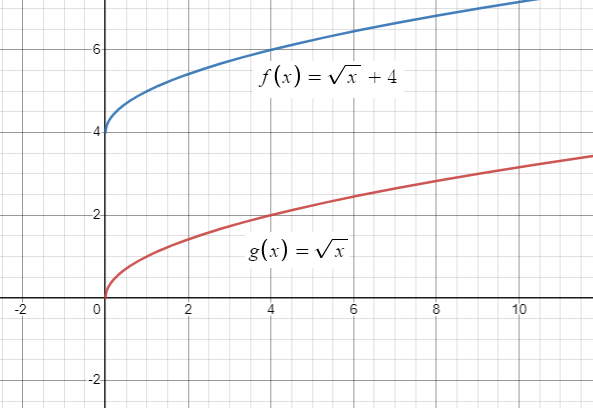
Problem 4 :

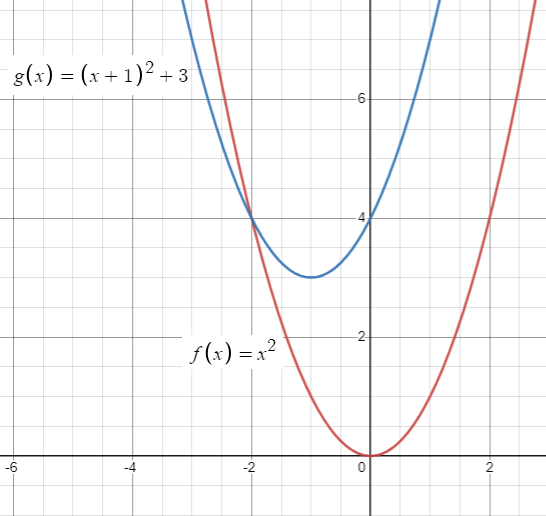
g(x) = (x + 1)² + 3

Solution :

By observing the function g(x), the highest exponent is 2. So, it is a quadratic function, its graphical form will be in the shape of U.

Parent function :

f(x) = x²

Transformation :

g(x) = (x - (-1))² + 3

Comparing with the parent function, in the function g(x), h = -1 and k = 3. So, move the graph f(x) 1 unit left and 3 units up.

Problem 5 :

g(x) = x - 2

Solution :

By observing the function g(x), the highest exponent is 1. So, it is a linear function, its graphical form will be a straight line.

Parent function :

f(x) = x

Transformation :

g(x) = x - 2

Comparing with the parent function, in the function g(x), k = -2. So, move the graph f(x) 2 units down.

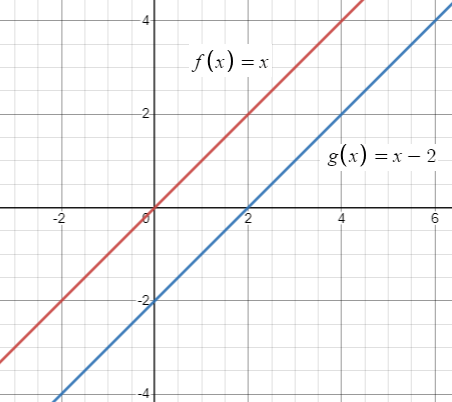
Problem 6 :

g(x) = |x + 5| - 2

Solution :

By observing the function g(x), the highest exponent is 1 and it is inside the absolute sign. It is a absolute value function and its graphical form will be the shape of V.

Parent function :

f(x) = x

Transformation :

g(x) = |x - (-5)| - 2

Comparing with the parent function, in the function g(x), h = -5 and k = -2. So, move the graph f(x) 5 units left and 2 units down.

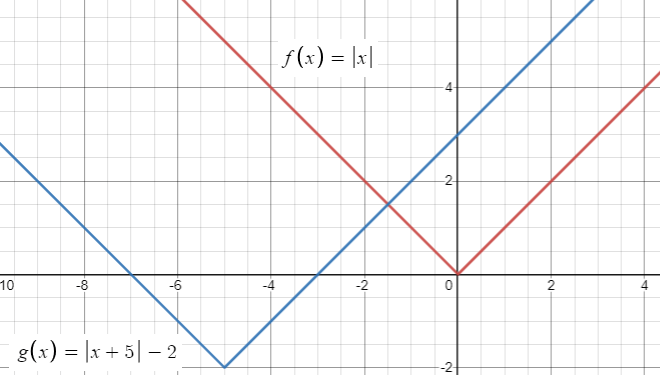
Problem 7  :

g(x) =  √(x+2) - 5

Solution :

By observing the function g(x), it must be a square root function.

Parent function :

f(x) =√x

Transformation :

g(x) = √(x - (-2)) - 5

Comparing with the parent function, in the function g(x), h = -2 and k = -5. So, move the graph f(x) 2 units left and 5 units down.

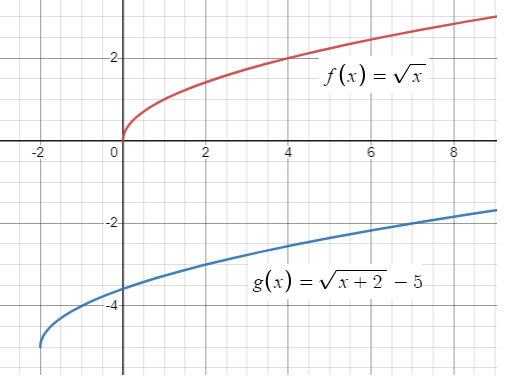
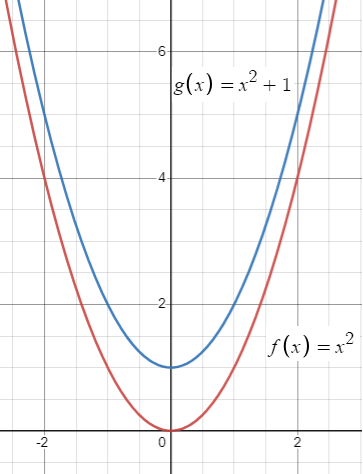
Problem 8  :

g(x) = x² + 1

Solution :

By observing the function g(x), the highest exponent is 2. So, it is a quadratic function, its graphical form will be in the shape of U.

Parent function :

f(x) = x²

Transformation :

g(x) = x² + 1

Comparing with the parent function, in the function g(x),k = 1. So, move the graph f(x) 1 unit up.

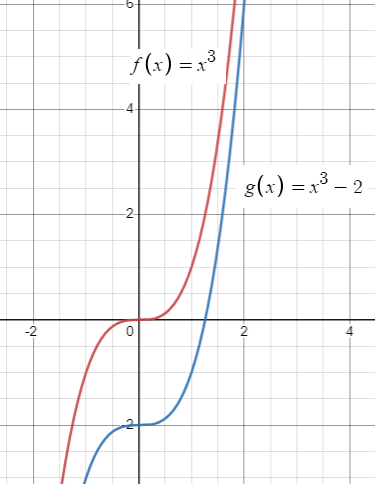
Problem 9  :

g(x) = x³ - 2

Solution :

Parent function :

f(x) = x³

Transformation :

g(x) = x³ - 2

The parent function should be moved 2 units down.