TRANSLATING VERBAL EXPRESSIONS TO ALGEBRAIC EXPRESSIONS

Problem 1 :

Write each verbal phrase as an algebraic expression.

1) the sum of 8 and t

2) the quotient of g and 15

3) the product of 5 and b

4) the difference of 32 and x

Solution :

1) Sum = +

Required expression : 8 + t

2) Quotient = /

Required expression : g/15

3) Product = x

Required expression : 5 x b

4) Difference = -

Required expression : 32 - x

Problems 2 :

Translate the verbal phrase to algebraic equations.

Problem 3 :

Arthur is 8 years younger than Janet

Solution :

Let A be Arthur's age. Janet's age be J.

Arthur's age is 8 less than Janet's age. Because Janet is elder.

A = J - 8

Problem 4 :

Kelly’s test score is 6 points higher than Mike’s

Solution :

Let K be Kell's test score. M be Mike's test score.

K = M + 6

Problem 5 :

5 more than a number is 6.

Solution :

Let x be the unknown.

More than = +

5 + x = 6

Problem 6 :

The product of 7 and b is equal to 63.

Solution :

Product of = x 

7 x b = 63

Problem 7 :

The sum of r and 45 is 79.

Solution :

Sum of = +

r + 45 = 79

Problem 8 :

The quotient of x and 7 is equal to 13.

Solution :

Quotient = /

x/7 = 13

Problem 9 :

In a cross-country race you run at a steady rate of 7 minutes per mile. After 21 minutes, you finish in fourth place. How long is the race?

Solution :

The time taken to cover 1 mile = 7 minutes

Total time taken to finish the race = 21 minutes

Duration of race time = 21/7

= 3 minutes

Problem 10 :

For a science project, you record the high temperature each day. The high temperature on Day 1 was 6° less than on Day 4 and 4° less than on Day 10. The high temperature on Day 10 was 62°F. What was the high temperature on Day 1?

Solution :

Temperature on Day 10 = 62°F

Temperature on Day 4 = 62 - 4

= 58°F

Temperature on Day 1 = 58 - 6

= 52°F

So, the temperature on Day 1 is 52°F.

Problem 11 :

Students and faculty raised $6042 for band uniforms. The faculty raised $1780. Write an equation you can use to find the amount a raised by the students.

Solution :

Total amount raised = 6042

Amount raised by faculty = 1780

Amount raised by students = x

x + 1780 = 6042

x = 6042 - 1780

x = 4262

So, the required amount raised by the students is $4262.

Problem 12 :

Together you and a friend have $52. Your friend has $28. Write an equation you can use to find how much money you have.

Solution :

The amount you have = x

The amount your friend have = 28

Total money = 52

x + 28 = 52

x = 52 - 28

x = 24

So, the amount you have is $24.

Problem 12 :

You hit a golf ball 90 yards. It travels three-fourths of the distance to the hole. Write an equation you can use to find the distance d from the tee to the hole.

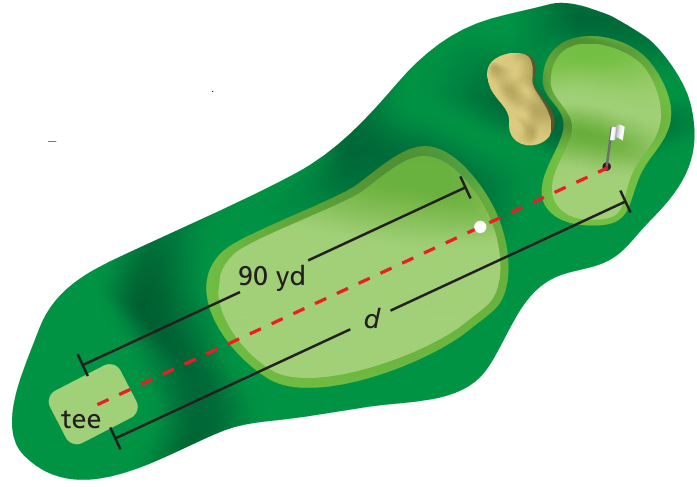
Solution :

Total distance from tee to the target is d yards.

3/4 of d = 90

(3/4)d = 90

3d/4 = 90

3d = 90(4)

3d = 360

d = 360/3

d = 120 yards.

Problem 13 :

Which expression is equivalent to 8(x + 3)?

a) 8x + 3      b) 8x + 24     c) 8x + 11      d) x + 24

Solution :

Using distributive property, multiplying 8 by x + 3, we get

= 8x + 8(3)

= 8x + 24

So, option b is correct.

Problem 14 :

Evaluate the expression when a = 7

a)   6 + a       b)  a − 4        c)  4a      d) 35/a 

Solution :