TRANSLATING SENTENCE INTO EQUATIONS

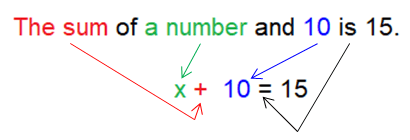
Let  x represent  the number. Use mental math to solve the equation. 

Problem 1 :

The sum of a number and 10 is 15.

Solution :

Let x be the number.

x + 10 = 15

Subtract 10 on both sides.

x = 15 - 10

x = 5

Problem 2 :

28 decreased by a number is18.

Solution :

Let x be the number.

28 - x = 18

Subtract 28 on both sides.

-x = 18 - 28

-x = -10

x = 10

Problem 3 :

The product of a number and 25 is 100.

Solution :

Let x be the number.

x ∙ 25 = 100

Divide by 25 on both sides.

x = 100/25

x = 4

Problem 4 :

The quotient of 49 and a number is 7.

Solution :

Let x be the number.

49/x = 7

Multiply by x on both sides.

49 = 7x

Divide by 7 on both sides.

x = 49/7

x = 7

Problem 5 :

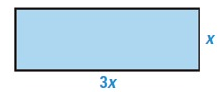
The area of the rectangle is less than or equal to 50 meters. Write an inequality for the area using the dimensions in the diagram.

Solution:

Let the width of rectangle is x meter.

Length is 3x meter.

Area of rectangle = Length × Width

= 3x ∙ x

Area = 3x²

As per the question,

3x² ≤ 50

Problem 6 :

The distance between your house and the amusement park s 110 miles. Your rate of travel is 55 miles per hour. Use the formula d = rt to write an equation. Use mental math to solve the equation for the time you spend traveling.

Solution :

Given,

Distance d = 110 miles

rate r = 55 miles per hour

Use the formula d = rt

time = d/r

t = 110/55

time = 2 hours

Problem 7 :

Translate into mathematical symbols “the difference of a number and 4 is 10”. Let n represent the number.

A)  n - 4 = 10    B)  4 - n = 10    C)  10 - 4 = n    D)  10 – n = 4

Solution :

Given, the difference of a number and 4 is 10.

That is,

n – 4 = 10

So, option (A) is correct.

Problem 8 :

Which is the correct algebraic translation of “Howard’s hourly wage h is $2 greater them Marla’s hourly wage m?”

A)  h < m+2   B)  h = m+2   C)  m = h+2   D)  h > m+2

Solution :

Given, Howard’s hourly wage h is $2 greater them Marla’s hourly wage m.

That is,

 h > m+2

So, option (D) is correct.

Problem 9 :

Find the volume of a cube when each side x is 10 feet.

Solution :

We know, volume of a cube = (side x side x side)

Here, side = 10 feet

= 10x10x10

= 1000

Therefore, volume of a cube = 1000 feet³

Problem 10 :

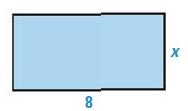
The rectangle shown at the right has an area of 32 square units. Write an equation to find the width x.

Solution :

Given,

Area = 32 square units

Length = 8 and Width = x

Area of a Rectangle = length x width

Width = Area/length

x = 32/8

x = 4

So, width x = 4.

Problem 11 :

The perimeter of the parallelogram is 102 feet. Find m.

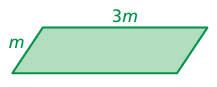
Solution :

Perimeter of parallelogram = 102 feet

m + 3m + m + 3m = 102

2m + 6m = 102

8m = 102

m = 102/8

m = 12.5

Problem 12 :

On Saturday, you catch insects for your science class. Five of the insects escape. The remaining insects are divided into three groups to share in class. Each group has nine insects. How many insects did you catch on Saturday?

a. Solve the problem by working backwards.

b. Solve the equation (x − 5)/3 = 9. How does the answer compare with the answer to part (a) ?

Solution :

a) After five insects escaped, the remaining insects are divided into groups.

Number of groups = 3

Number of insects in each group = 9

Working backwords,

total number of insects = 3 x 9 + 5

= 27 + 5

= 32 insects

b) (x − 5)/3 = 9

Multiplying by 3, we get

x - 5 = 9(3)

x - 5 = 27

Adding 5 on both sides, we get

x = 27 + 5

x = 32

Problem 13 :

You must scuba dive to the entrance of your room at Jules’ Undersea Lodge in Key Largo, Florida. Entrance The diver is 1 foot deeper than 2/3 of the elevation of the entrance. What is the elevation of the entrance?

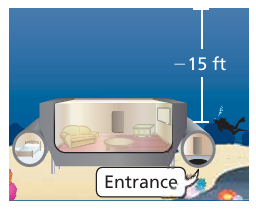
Solution :

Let x be the elevation of the entrance.

(2/3) of x - 1 = -15

(2x/3) - 1 = -15

(2x/3) = -15 + 1

2x/3 = -14

2x = -14(3)

2x = -42

x = -42/2

x = -21 feet

Problem 12 :

How much should you change the width of the rectangle so that the perimeter is 54 centimeters? Write an equation that shows how you found your answer

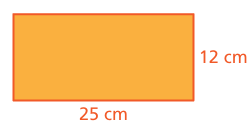
Solution :

Perimeter of the given rectangle = 2(25 + 12)

= 2(37)

= 74

The perimeter of the rectangle should be 54.

Let x be the quantity should be subtracted from width.

2(25 + 12 - x) = 54

2(37 - x) = 54

37 - x = 54/2

37 - x = 27

-x = 27 - 37

-x = -10

x = 10

So, we should subtract 10 from the given width.