TRANSFORMATION OF SQUARE ROOT FUNCTION WORKSHEET

Graph each transformation of the parent function

f(x) = √x

Analyze the effect of the transformation on the graph of the parent function

Problem 1 :

y = (1/4)√x 

Solution

Problem 2 :

y = -2√x 

Solution

Problem 3 :

y = 3√(x + 2)

Solution

Problem 4 :

y = √-5x

Solution

Problem 5 :

y = √2x + 1

Solution

Problem 6 :

A company makes steel food cans of different sizes. All of the cans are 10 cm tall, but their radii vary. The equation r = 0.18√V gives the radius of a can based on the can’s volume.

a. Describe this equation as a transformation of y = √x.

b. The volume of one size of can is 300 cubic centimeters. What is the radius of this can? Round to the nearest hundredth.

Solution

Problem 7 :

The quality control supervisor at a car part factory uses the equation

y = √ (1/10) x + 20

to determine the number of parts, y, to inspect based on the number manufactured, x.

a. Describe this equation as a transformation of y = √x.

b. The supervisor determined that 55 parts should be inspected. How many were manufactured?

Solution

Answer Key

1)  0 < a < 1, there is vertical shrink of 1/4 units.

x 0 1 4 9

y = (1/4)√x  y = (1/4)√0 = 0  y = (1/4)√1 = 0.25 y = (1/4)√4 = 0.5 y = (1/4)√9 = 0.75

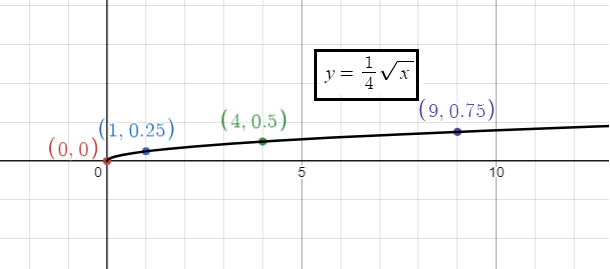
2)  a > 1, there is vertical stretch of 2 units.

x 0 1 4 9

y = -2√x  y = -2√0 = 0 y = -2√1 = -2 y = -2√4 = -4 y = -2√9 = -6

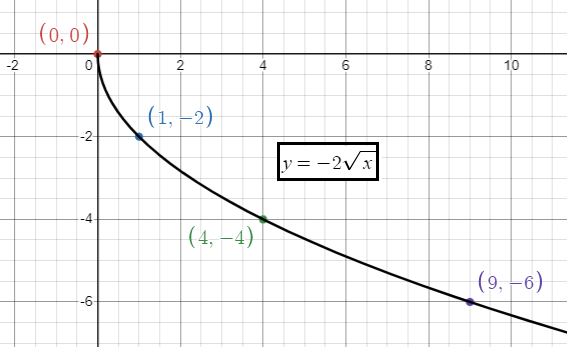
3)

•  a > 3, there is vertical stretch of 3 units.
• h = -2, move the graph horizontally 2 units left.

x 0 1 2 7

y = 3√(x + 2) y = 3√2 = 4.24 y = 3√(1 + 2) = 5.196 y = 3√(2 + 2) = 6 y = 3√(7 + 2) = 9

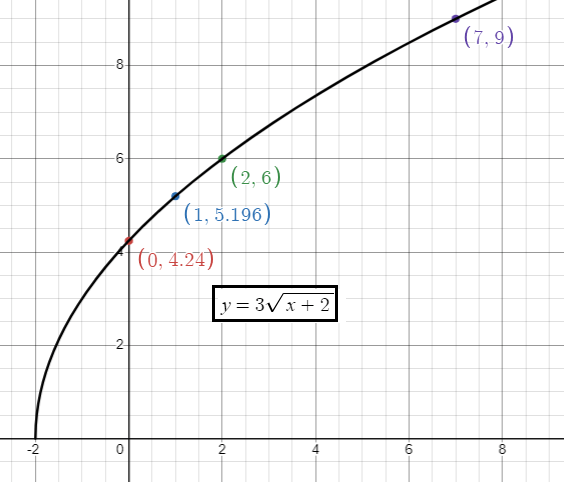
4) 

• b = 5 > 1, there is horizontal compression.
• Sign of b is negative, so there is a reflection across y-axis.

x 0 -1 -5

y = √(-5x) y = √(-5(0)) = 2 y = √(-5(-1)) = 2.23 y = √(-5(-5)) = 5

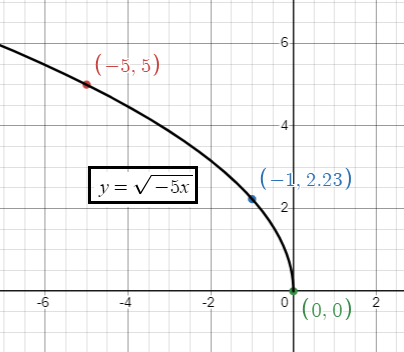
5)  

• b = 2 > 1, there is horizontal compression.
• k = 1, move the graph up 1 unit.

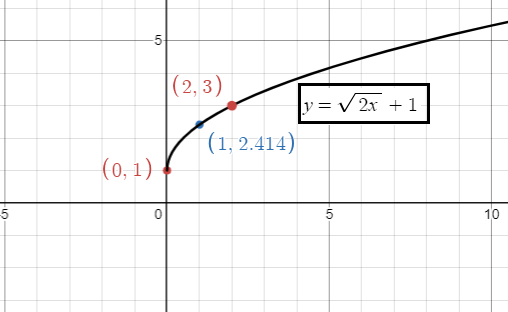
6)  a)  There is vertical compression of 0.18 units.

b) r = 3.117

7)  a) Here b = 1/10

b)  x = 12250