TANGENTS FROM AN ECTERNAL POINT TO A CIRCLE WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
If the angle between two tangents drawn from an external point 𝑃 to a circle of radius 𝑎 and center 𝑂, is 60°, then find the length of 𝑂𝑃.
Problem 2 :
𝑃𝑄 is a tangent drawn from an external point 𝑃 to a circle with center 𝑂, 𝑄𝑂𝑅 is the diameter of the circle. If ∠ 𝑃𝑂𝑅 = 120°, what is the measure of ∠𝑂𝑃𝑄?
Problem 3 :
In the given figure 𝑃𝐴 and 𝑃𝐵 are tangents to a circle with center 𝑂. If ∠𝐴𝑃𝐵 = (2𝑥 + 3)° and ∠𝐴𝑂𝐵 = (3𝑥 + 7)°, then find the value of 𝑥.
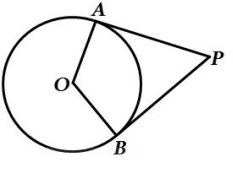
Problem 4 :
In figure, 𝑃𝑄 is a tangent at a point 𝐶 to a circle with center 𝑂. If 𝐴𝐵 is a diameter and ∠𝐶𝐴𝐵 = 30°, find ∠𝑃𝐶𝐴.
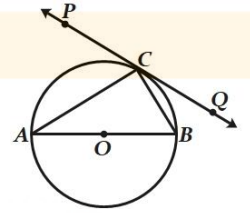
Problem 5 :
In figure, 𝐴𝑂𝐵 is a diameter of a circle with centre 𝑂 and 𝐴𝐶 is a tangent to the circle at 𝐴. If ∠𝐵𝑂𝐶 = 130°, then find ∠𝐴𝐶𝑂.
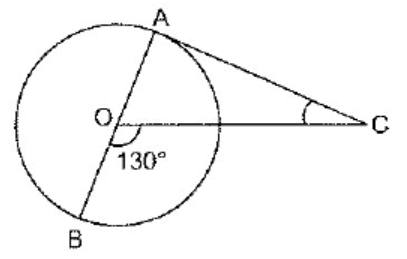
Problem 6 :
In figure, 𝑃𝐴 and 𝑃𝐵 are tangents to the circle with center 𝑂 such that ∠𝐴𝑃𝐵 = 50°. Write the measure of ∠𝑂𝐴B
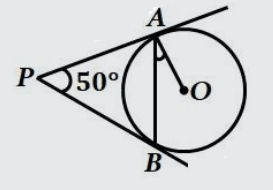
Problem 7 :
In figure, 𝑃𝐴 and 𝑃𝐵 are two tangents drawn from an external point 𝑃 to a circle with center 𝐶 and radius 4 𝑐𝑚. If 𝑃𝐴 ⊥ 𝑃𝐵, then the length of each tangent is:
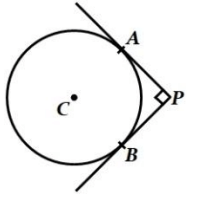
Problem 8 :
In figure, the sides 𝐴𝐵,𝐵𝐶 and 𝐶𝐴 of a triangle 𝐴𝐵𝐶, touch a circle at 𝑃, 𝑄 and 𝑅 respectively. If 𝑃𝐴 = 4 𝑐𝑚, 𝐵𝑃 = 3 𝑐𝑚 and 𝐴𝐶 = 11 𝑐𝑚, then the length of 𝐵𝐶 (in 𝑐𝑚) is:
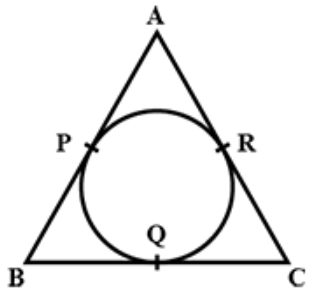
Problem 9 :
In figure, a circle touches the side 𝐷𝐹 of Δ𝐸𝐷𝐹 at 𝐻 and touches 𝐸𝐷 and 𝐸𝐹 produced at 𝐾 and 𝑀 respectively. If 𝐸𝐾 = 9 𝑐𝑚, then the perimeter of Δ𝐸𝐷𝐹 (in 𝑐𝑚) is:
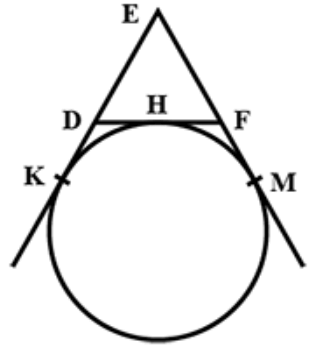
Problem 10 :
In figure, 𝑃𝑄 and 𝑃𝑅 are tangents to a circle with center 𝐴. If ∠𝑄𝑃𝐴 = 27°, then ∠𝑄𝐴𝑅 equals.
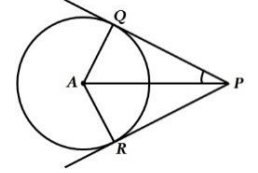
Answer Key
1) length of OP is 2a.
2) ∠OPQ = 30
3) x = 34
4) ∠ABC = 60
5) ∠ACO = 40
6) ∠BAO = 25
7) AC = AP = 4 cm
8) BC = 10 cm
9) 18 cm
10) ∠𝑄𝐴R = 126
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling