SYSTEM OF SIMULTANEOUS LINEAR EQUATIONS WITH FRACTIONAL COEFFICIENTS

To solve system of linear equations, we may use different methods :

Using elimination method :

• Write the given equations in standard form.
• Compare the coefficients of the variables that we are planning to eliminate.
• If the coefficients are same and they have opposite signs, by adding those two equations, we can eliminate the variable.
• If the coefficients are not same, multiply it by some constants and make it same.

More example problems

Using substitution method :

To use this method, we have to take one of the equations and solve for one variable in terms of other variable.

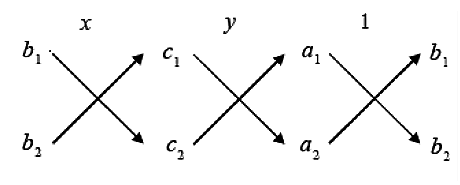
Cross multiplication method :

The given equations should be in the form,

a₁ x + b₁y + c₁ = 0

a₂ x + b₂y + c₂ = 0

Solve the following pairs of simultaneous equations:

Problem 1 :

2x + 1/3y = 1

3x + 5y = 6

Solution:

2x + 1/3y = 1 ---> (1)

3x + 5y = 6 ---> (2)

Multiply the equation (1) by 3, we get

6x + y = 3 ---> (3)

Multiply the equation (2) by 2, we get

6x + 10y = 12 ---> (4)

Subtracting equation (3) & (4)

-9y = -9

y = 1

By applying y = 1 in equation (2)

3x + 5(1) = 6

3x + 5 = 6

3x = 1

x = 1/3

So, the solution is x = 1/3 and y = 1.

Problem 2 :

4x + 3y = 5

2x - 3/4y = 1

Solution :

4x + 3y = 5 ---> (1)

2x - 3/4y = 1 ---> (2)

Multiply the equation (2) by 4, we get

8x - 3y = 4 ---> (3)

Adding equation (1) & (3)

12x = 9

x = 3/4

By applying x = 3/4 in equation (1)

4(3/4) + 3y = 5

3 + 3y = 5

3y = 2

y = 2/3

So, the solution is x = 3/4 and y = 2/3.

Problem 3 :

1/3x + y = 10/3

2x + 1/4y = 11/4

Solution:

1/3x + y = 10/3 ---> (1)

2x + 1/4y = 11/4 ---> (2)

Multiply the equation (1) by 3, we get

x + 3y = 10 ---> (3)

Multiply the equation (2) by 4, we get

8x + y = 11 ---> (4)

(4) × 3 ==> 24x + 3y = 33 ---> (5)

Subtract equation (3) & (5)

-23x = -23

x = 1

By applying x = 1 in equation (1)

1/3(1) + y = 10/3

1/3 + y = 10/3

y = 9/3

y = 3

So, the solution is x = 1 and y = 3.

Problem 4 :

3x - 2y = 5/2

1/3x + 3y = -4/3

Solution:

3x - 2y = 5/2 ---> (1)

1/3x + 3y = -4/3 ---> (2)

Multiply the equation (2) by 3, we get

x + 9y = -4 ---> (3)

(3) × 3 ==> 3x + 27y = -12 ---> (4)

Subtracting equation (1) & (4)

-29y = 29/2

y = -1/2

By applying y = -1/2 in equation (1)

3x - 2(-1/2) = 5/2

3x + 1 = 5/2

3x = 3/2

x = 1/2

So, the solution is x = 1/2 and y = -1/2.

Problem 5 :

x = 1/3y

2y - 6x = 9

Solution:

x = 1/3y ---> (1)

2y - 6x = 9 ---> (2)

By applying x = 1/3y in equation (2)

2y - 6(1/3y) = 9

2y - 2y = 9

0 = 9

So, there is no solution.

Problem 6 :

(4/3) + (5x/4) = 28y + (5x/8)

my = (1/2)(5x - 8)

In the given system of equations, m is a constant. If the system has no solution. What is the value of m ?

Solution :

(4/3) + (5x/4) = 28y + (5x/8) ------(1)

my = (1/2)(5x - 8) ------(2)

Since the system of equation has no solution, they will not intersect each other and 

From (1)

28y = (5x/4) - (5x/8) + (4/3)

28y = (10x - 5x)/8 + (4/3)

28y = (5x/8) + (4/3)

y = (5x/8 ⋅ 28) + (4/3 ⋅ 28)

y = (5x/224) + (1/21)

Slope (m₁) = 5/224

y-intercept (b₁) = 1/21

From (2)

my = (1/2)(5x - 8)

y = (1/2m)(5x - 8)

= (5/2m)x - (8/2m)

y = (5/2m)x - (4/m)

Slope (m₂) = 5/2m

y-intercept (b₂) = -4/m

m₁ = m₂

5/224 = 5/2m

5(2m) = 5(224)

m = 112

m = 112

Problem 7 :

If (x + y)/x = 9 and ay/3x = 32 where a is a constant. What is the value of a ?

Solution :

(x + y)/x = 9 and ay/3x = 32

x + y = 9x

x - 9x + y = 0

-8x + y = 0 ------(1)

ay/3x = 32

y = 32(3x)/a

y = 96x/a

Applying the value of y in (1), we get

-8x + (96x/a) = 0

-8ax + 96x = 0

-8ax = -96x

a = 96/8

a = 12

So, the value of a is 12.

Problem 8 :

mx - 6y = 10

2x - ny = 5

In the given system of equations m and n are constants. The system has infinitely many solutions. What is the value m/n ?

a)  1/12      b)  1/3      c)  4/3     d)  3

Solution :

mx - 6y = 10 ------(1)

2x - ny = 5 ------(2)

Since the system has infinitely many solution, their slopes and y-intercepts will be equal.

When n = 3, m = 4

m/n = 4/3

So, the value of m/n is 4/3.