SYNTHETIC POLYNOMIAL DIVISION FOR SAT PRACTICE

Problem 1 :

The expression 

is equal to which of the following ?

Solution :

We cannot divide the polynomials using long division, because it is not an improper fraction.

Simplifying option b :

Simplifying option c :

So, option c is correct.

Problem 2 :

If the expression

is written in the form 

what us Q in terms of x ?

(a)  3x - 1    (b) 3x + 1    (c)  6x² + 3x + 1    (c)  6x² + 5x + 1

Solution :

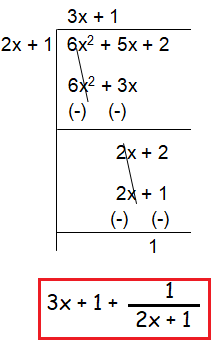
So, the value of Q is 3x + 1.

Problem 3 :

The expression 4x² + 5 can be written as A(2x - 1) + R, where A is an expression in terms of x and R is constant. What is the value of R?

Solution :

Using long division,

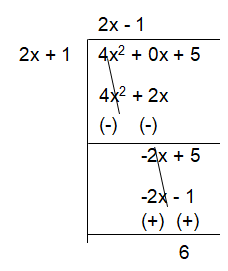
Using division algorithm,

Dividend = divisor x quotient + remainder

= (2x - 1)(2x + 1) + 6

The value of R is 6.

Problem 4 :

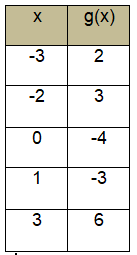
The function g is defined by a polynomial. The table above shows some values of x and g(x). What is the remainder when g(x) is divided by x + 3 ?

(a)  -2    (b)  1    (c)  2    (d)  6

Solution :

When x + 3 =0

x = -3

When the polynomial divided by x + 3, we get the remainder 2.

Problem 5 :

2z³ - kxz² + 5xz + 2x - 2

In the polynomial above, k is constant. If z - 1 is a factor of the polynomial above, what is the value of k ?

Solution : 

z - 1 = 0

z = 1

Let p(z) = 2z³ - kxz² + 5xz + 2x - 2

p(1) = 2(1)³ - kx(1)² + 5x(1) + 2x - 2

p(1) = 2 - kx + 5x + 2x - 2

0 = -kx + 7x

k = 7

Problem 6 :

When 3x² - 8x - 4 is divided by 3x - 2, the result can be expresses as 

What is A in terms of x ?

(a)  x - 4     (b)  x - 2    (c) x + 2   (d) x + 4

Solution :

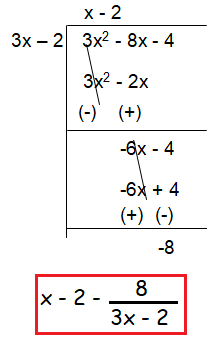
So, the value of A is x - 2.

Problem 7 :

The expression 2x² - 4x - 3 can be written as A(x + 1) + B, where B is constant. What is A in terms of x ?

(a)  2x + 6     (b)  2x + 2    (c) 2x - 2    (d) 2x - 6

Solution :

From the question, it is clear that 2x² - 4x - 3 should be divided by x + 1

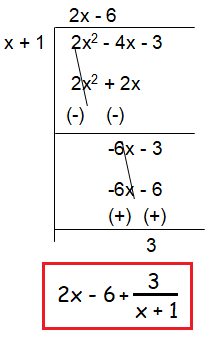
So, the value of A is 2x - 6.

Problem 8 :

The expression x² + 4x - 9 can be written as (ax + b)(x - 2) + c, where a, b and c are constants. What is the value of a + b + c ?

(a)  -2     (b)  3    (c) 7    (d) 10

Solution :

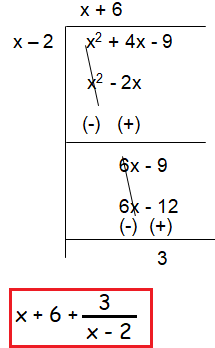
ax + b = x + 6 and c = 3

a = 1, b = 6 and c = 3

a + b + c = 1 + 6 + 3 ==> 10

So, the answer is 10.

Problem 9 :

For a polynomial p(x), p(2) = 0. Which of the following must be true about p(x) ?

(a) 2x is a factor of p(x)      (b)  2x - 2 is a factor of p(x)

(c)  x - 2 is a factor of p(x)     (d)  x + 2 is a factor of p(x)

Solution :

p(2) = 0

x = 2

x - 2

Then x - 2 is a factor.

Problem 10 :

If p(x) = x³ + x² - 5x + 3, then p(x) is divisible by which of he following ?

I.  x - 2       II.  x - 1   III. x + 3

(a) I and II only        (b)  I and III only

(c)  II and III only       (d)  I, II and III

Solution :

I. x - 1

x - 1 = 0

x = 1

Let us check if x - 1 is a factor of the polynomial, p(x).

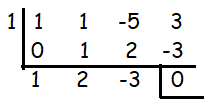
x - 1 is a factor.

II. x - 2

x - 2 = 0

x = 2

Let us check if x - 2 is a factor of the polynomial, p(x).

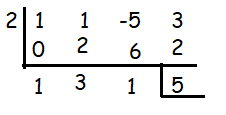
x - 2 is not a factor.

III. x + 3

x + 3 = 0

x = -3

Let us check if x + 3 is a factor of the polynomial, p(x).

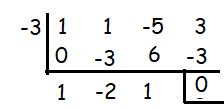
x + 3 is a factor.

So, I and III are factors.

Problem 11 :

If the polynomial p(x) is divisible by x - 2, which of the following could be p(x)

(a) p(x) = -x² + 5x - 14       (b) p(x) = x² - 6x - 2 

(c)  p(x) = 2x² + x - 8      (d)  p(x) = 3x² - 2x - 8 

Solution :

Option (a) :

p(x) = -x² + 5x - 14

p(x) = -(x² - 5x + 14)

p(x) = -(x - 7)(x + 2)

Option (b) :

p(x) = x² - 6x - 2

Since it is not factorable, x - 2 is not a factor.

Option (d) :

p(x) = 3x² - 2x - 8

p(x) = (3x² - 6x + 4x - 8)

p(x) = 3x(x - 2) + 4(x - 2)

p(x) = (3x + 4)(x - 2)

So, the factor of 3x² - 2x - 8 is x - 2.

Problem 12 :

If x - 1 and x + 1 are both factors of the polynomial

ax⁴ + bx³ - 3x² + 5x

and a and b are constants, what is the value of a ?

(a)  -3    (b)  1      (c) 3     (d)  5

Solution :

Let p(x) = ax⁴ + bx³ - 3x² + 5x

x - 1 is a factor, then x = 1 is a solution.

p(1) = a(1)⁴ + b(1)³ - 3(1)² + 5(1)

0 = a + b - 3 + 5

a + b = -2 -----(1)

x + 1 is a factor, then x = -1 is a solution.

p(-1) = a(-1)⁴ + b(-1)³ - 3(-1)² + 5(-1)

0 = a - b - 3 - 5

a + b = 8 -----(2)

(1) + (2)

2a = 6

a = 3

So, the answer is 3.

Problem 13 :

For a polynomial p(x), p(1/3) = 0. Which of the following must be a factor of p(x)

(a)  3x - 1    (b)  3x + 1      (c) x - 3     (d)  x + 3

Solution :

Since 1/3 is a zero of the polynomial.

x = 1/3 is a solution.

Converting it as factor, we get x - 1/3

(3x - 1) is a factor of p(x)