SURFACE AREA OF SIMILAR SOLIDS

If two figures are similar then:

• the figures are equiangular, and
• the corresponding sides are in proportion.

Surface area of similar figures :

If two solids are similar, then the ratio of their surface areas is equal to the square of the ratio of their corresponding linear measures. 

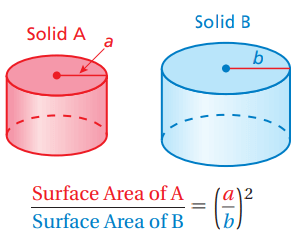
Each pair of figures is similar. Use the information given to find the scale factor of the figure on the left to the figure on the right. 

Problem 1 :

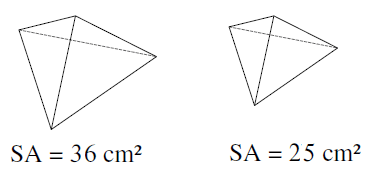
Solution :

Surface area of large shape : Surface area of small shape

= 36 : 25

k² = 36/25

k = √36/25

k = 6/5

So, the scale factor is 6 : 5.

Problem 2 :

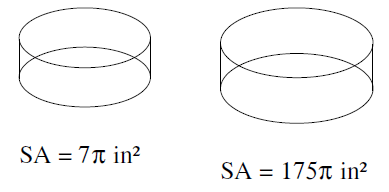
Solution :

Surface area of small shape : Surface area of large shape

= 7π : 175π

k² = 7π/175π

k² = 1/25

k = √1/25

k = 1/5

So, the scale factor is 1 : 5.

Problem 3 :

The solids are similar. Find the surface area S of the shaded shape.

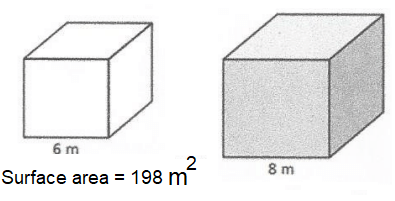
Solution :

Let l = side length of small cube

L = Side length of large cube

s = surface area of small cube

S = surface area of large cube

s : S = (l : L)²

198/S = (6/8)²

198/S = 36/64

Doing cross multiplication,

S = (198 ⋅ 64)/36

S = 352 m²

Problem 4 :

The pyramids are similar. What is the surface area of Pyramid A?

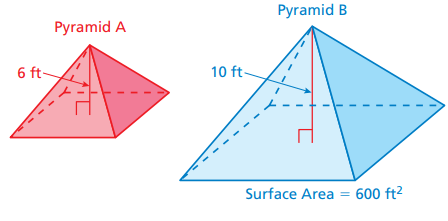
Solution :

Let h = height of small pyramid

H = height of large pyramid

s = surface area of small pyramid

S = surface area of large pyramid

s : S = (h : H)²

s : 600 = (6/10)²

s : 600 = 36/100

s = (36/100) ⋅ 600

s = 216 ft²

Problem 5 :

Find the surface area of smaller cuboid.

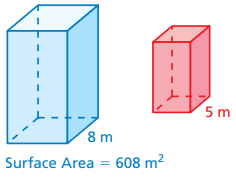
Solution :

Let w = width of cuboid

W = width of cuboid

s = surface area of small cuboid

S = surface area of large cuboid

s : S = (w : W)²

s : 608 = (5/8)²

s : 608 = 25/64

s = (25/64) ⋅ 608

s = 237.5 m²

Problem 6 :

Find the surface area of large cylinder.

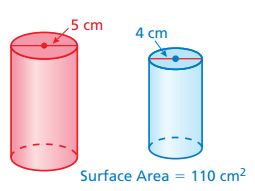
Solution :

Let R = radius of large cylinder = 5/2

r = radius of small cylinder = 2

s = surface area of small cylinder = 110 cm²

S = surface area of large cylinder

s : S = (r : R)²

110 : S = (2/(5/2))²

110 : S = (4/5)²

110 : S = (4/5)²

110/S = 16/25

S = 110(25/16)

S = 171.875 cm²