SUM OF INTERIOR ANGLES OF A TRIANGLE

Find the value of ‘’x’’.

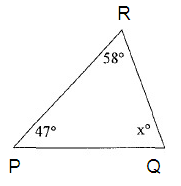
Problem 1 :

Solution :

In triangle PQR, the sum of interior angles is 180^º.

∠P + ∠Q + ∠R = 180^º

47^º + x^º + 58^º = 180^º

105^º + x^º = 180^º

Subtract 105^º from both sides.

105^º - 105^º + x^º = 180^º - 105^º

x^º = 75^º

So, the value of x is 75^º.

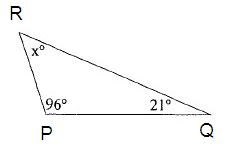
Problem 2 :

Solution :

In triangle PQR, the sum of interior angles is 180^º.

∠P + ∠Q + ∠R = 180^º

96^º + 21^º + x^º = 180^º

117^º + x^º = 180^º

Subtract 117^º from both sides.

117^º - 117^º + x^º = 180^º - 117^º

x^º = 63^º

So, the value of x is 63^º.

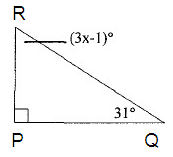
Problem 3 :

Solution :

In triangle PQR, the sum of interior angles is 180^º.

∠P + ∠Q + ∠R = 180^º

90^º + 31^º + (3x – 1)^º = 180^º

90^º + 31^º + 3x^º – 1^º = 180^º

120^º + 3x^º = 180^º

Subtract 120^º from both sides.

120^º - 120^º + 3x^º = 180^º - 120^º

3x^º = 180^º - 120^º

3x^º = 60^º

Divide both sides by 3.

3x^º/3 = 60^º/3

x^º = 20

So, the value of x is 20^º.

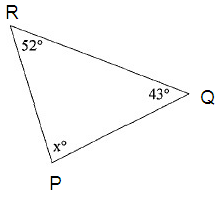
Problem 4 :

Solution :

In triangle PQR, the sum of interior angles is 180^º.

∠P + ∠Q + ∠R = 180^º

x^º + 43^º + 52^º = 180^º

95^º + x^º = 180^º

Subtract 95^º from both sides.

95^º - 95^º + x^º = 180^º - 95^º

x^º = 85^º

So, the value of x is 85^º.

Problem 5 :

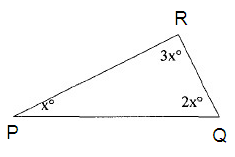
Solution :

In triangle PQR, the sum of interior angles is 180^º.

∠P + ∠Q + ∠R = 180^º

x^º + 2x^º + 3x^º = 180^º

6x^º = 180^º

Divide both sides by 6.

6x^º/6 = 180^º/6

x^º = 30^º

So, the value of x is 30^º.

Problem 6 :

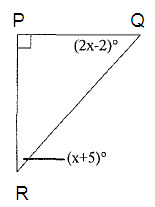
Solution :

In triangle PQR, the sum of interior angles is 180^º.

∠P + ∠Q + ∠R = 180^º

90^º + (2x – 2)^º + (x + 5)^º = 180^º

90^º + 2x^º – 2^º + x^º + 5^º = 180^º

93^º + 3x^º = 180^º

Subtract 93^º from both sides.

93^º - 93^º + 3x^º = 180^º - 93^º

3x^º = 87^º

Divide both sides by 3.

3x^º/3 = 87^º/3

x^º = 29^º

So, the value of x is 29^º.

Problem 7 :

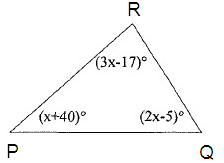
Solution :

In triangle PQR, the sum of interior angles is 180^º.

∠P + ∠Q + ∠R = 180^º

(x + 40)^º + (2x – 5)^º + (3x - 17)^º = 180^º

x^º  + 40^º + 2x^º – 5^º + 3x^º - 17^º = 180^º

18^º + 6x^º = 180^º

Subtract 18^º from both sides.

18^º - 18^º + 6x^º = 180^º - 18^º

6x^º = 162^º

Divide both sides by 6.

6x^º/6 = 162^º/6

x^º = 27^º

So, the value of x is 27^º.

Problem 8 :

A triangle whose one angle is more than 90˚ is called ------------

Solution :

If one of the angle which is more than 90 degree then it is called obtuse triangle.

Problem 9 :

A triangle whose all the sides are of different length is called ------------

Solution :

In a triangle,

• if three sides are equal, it is called equilateral triangle
• if two sides are equal, it is called isosceles triangle
• if all sides are different, it is called scalene triangle.

Problem 10 :

The sum of the lengths of the sides of a triangle is called its ----------

Solution :

The sum of lengths of all sides of a triangle is called its perimeter of triangle.

Problem 11 :

The sum of the lengths of two sides of a triangle is always ------------than the third side.

Solution :

Using triangle inequality theorem, the sum of lengths of two sides of a triangle is always greater than the third side.

Problem 12 :

An exterior angle and the adjacent interior angle form a ------------.

Solution :

An exterior angle and the adjacent interior angle form a linear pair.

Problem 13 :

The sum of all the angles of a triangle is -----------

Solution :

The sum of all the angles of a triangle is 180 degree.

Problem 14 :

In a right angled triangle the side opposite to the right angle is called ------------

Solution : 

The side which is opposite to the right angle is called hypotenuse.

Problem 15 :

A triangle can not have more than one -------- angle.

Solution :

• A triangle may have three acture angles
• A triangle may have one right angle
• A triangle may have more than one obtuse angle.

Problem 16 :

Find the value’of x in given figure.

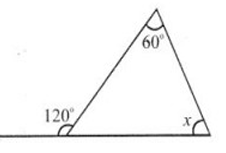
(a) 180°      (b) 55°       (c) 90°     (d) 60°

Solution :

Exterior angle = sum of remote interior angles

120 = 60 + x

120 - 60 = x

x = 60

So, the value of x is 60 degree.

Problem 17 :

An airplane leaves from Miami and travels around the Bermuda Triangle. What is the value of x?

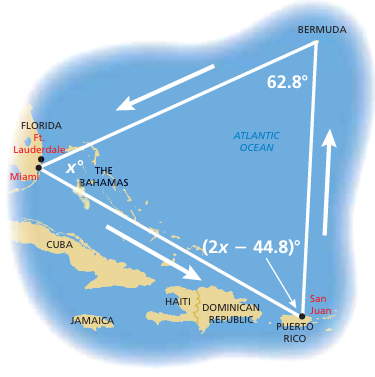
a) 26.8      b) 27.2      c) 54      d) 64

Solution :

x + 62.8 + 2x - 44.8 = 180

3x + 62.8 - 44.8 = 180

3x + 18 = 180

3x = 180 - 18

3x = 162

x = 162/3

x = 54

So, the value of x is 54.