SUM OF INTERIOR ANGLES OF A QUADRILATERAL

Find the unknown angles of a quadrilateral.

Problem 1 :

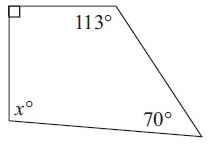
Solution :

Sum of interior angles = 360°

90° + 113° + 70° + x° = 360°

273° + x° = 360°

x° = 360° - 273°

x° = 87°

Problem 2 :

Solution :

Sum of interior angles = 360°

131° + 118° + 68° + x° = 360°

317° + x° = 360°

x° = 360° - 317°

x° = 43°

Problem 3 :

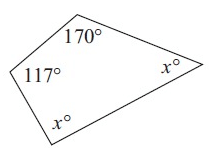
Solution :

Sum of interior angles = 360°

117° + 170° + x° + x° = 360°

287° + 2x° = 360°

2x° = 360° - 287°

2x° = 73°

x° = 73/2

x° = 36.5°

Problem 4 :

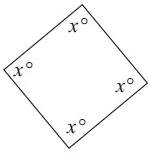
Solution :

Sum of interior angles = 360°

x° + x° + x° + x° = 360°

4x° = 360°

x° = 360°/4

x° = 90°

Problem 5 :

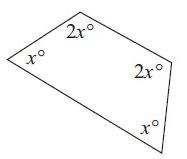
Solution :

Sum of interior angles = 360°

2x° + 2x° + x° + x° = 360°

6x° = 360°

x° = 360°/6

x° = 60°

Problem 6 :

One angle of a quadrilateral is 150°and other three angles are equal. What is the measure of each of these equal angles ?

(a) 75° (b) 85° (c) 95° (d) 70°

Solution :

Let x be those three angles.

Angels of quadrilateral are x, x, x and 150.

x + x + x + 150 = 360

3x + 150 = 360

Subtracting 150 on both sides.

3x = .360 - 150

3x = 210

Divide by 3 on both sides.

x = 210/3

x = 70

Problem 7 :

Four angles of quadrilateral are in the ratio 3:4:5:6. Find its angles.

Solution :

Let the four angles be 3x, 4x, 5x and 6x.

3x + 4x + 5x + 6x = 360

18x = 360

x = 360/18

x = 20

Problem 8 :

Three angles of a quadrilateral are 4 : 6 : 3. If the fourth angle is 100, find the three angles of a quadrilateral.

Solution : 

Let the three angles be 4x, 6x and 3x.

4x + 6x + 3x + 100 = 360

13x + 100 = 360

Subtracting 100 on both sides.

13x = 360 - 100

13x = 260

Dividing by 13 on both sides.

x = 260/13

x = 20

So, those three angles are 60, 80 and 120.

Problem 9 :

The sum of two angles of a quadrilateral is 160 the ratio 2 : 3. Find the angles.

Solution :

Sum of two angles of a quadrilateral = 160

Two angles are 2x and 3x

Sum of angles = 2x + 3x + 160

5x + 160 = 360

Subtracting 160 on both sides.

5x = 360 - 160

5x = 200

Dividing by 5 on both sides.

x = 200/5

x = 40

Problem 10 :

What is the maximum number of obtuse angles that a quadrilateral can have ?

(a) 1    (b) 2     (c) 3     (d) 4

Solution :

Total number of angles in a quadrilateral = 360

Sum of interior angle = 360

If we consider the three angles are having measures more than 90 degree, the fourth angle should be less than 90.

So, maximum three obtuse angles that quadrilateral can have.