SUM AND PRODUCT OF ROOTS OF QUADRATIC EQUATION WORD PROBLEMS WORKSHEET

Problem 1 :

Find the sum and product of the roots of :

3x² – 2x + 7 = 0

Solution

Problem 2 :

Find the sum and product of the roots of :

x² + 11x - 13 = 0

Solution

Problem 3 :

Find the sum and product of the roots of :

 5x² – 6x - 14 = 0

Solution

Problem 4 :

The equation kx² – (1 + k)x + (3k + 2) = 0 is such that the sum of its roots is twice their product. Find k and the two roots.               Solution

Problem 5 :

The quadratic equation ax² – 6x + a - 2 = 0, a ≠ 0, has one root which is double the other.

a) Let the roots be α and 2α. Hence find two equations involving α.

b)  Find α and the two roots of the quadratic equation.

Solution

Problem 6 :

Find the values of k for each of the following quadratic equations, so that they have two equal roots.

(i) 2x² + kx + 3 = 0

(ii) kx (x – 2) + 6 = 0

Solution

Problem 1 :

The quadratic equation kx² + (k–8)x + (1 – k) = 0, k ≠ 0, has one root which is two more than the other. Find k and the two roots.               Solution

Problem 2 :

The roots of the equation x² – 6x + 7 = 0 are α and β. Find the simplest quadratic equation with roots

α + 1/β and β + 1/α.

Solution

Problem 3 :

The roots of 2x² – 3x - 5 = 0 are p and q. Find all quadratic equations with roots p² + q and q² + p.

Solution

Problem 4 :

kx² + (k + 2) x - 3 = 0

has roots which are real and positive. Find the possible values that k may have.

Solution

Problem 1 :

Find the sum and product of roots of the quadratic equation

x² + 5x + 6 = 0

Solution

Problem 2 :

Find the sum and product of roots of the quadratic equation

x² - 4x - 10 = 0

Solution

Problem 3 :

Find the sum and product of roots of the quadratic equation

2x² + 6x + 8 = 0

Solution

Problem 4 :

Find the sum and product of roots of the quadratic equation

3x² + 5x - 9 = 0

Solution

Problem 5 :

Find the sum and product of roots of the quadratic equation

5x² - 7x - 10 = 0

Solution

Problem 6 :

Form the equation whose roots are 7and -10.

Solution

Find all values of k for which the equation has

(a) two solutions

(b) one solution and

(c) no solutions.

Problem 7 :

2x² + x + 3k = 0

Solution

Problem 8 :

x² − 4kx + 36 = 0

Solution

Problem 1 :

If a root of the equation

x² – 6x + k = 0 is 4

find the second root and the missing value.

Solution

Problem 2 :

Given the equation

x² + kx + 18 = 0

with one root of 6, find the second root and the missing value.

Solution

For these equations, one root is given. Find the second root and the missing value.

Problem 3 :

x² - x + k = 0, r₁ = -4

Solution

Problem 4 :

2x² + bx –15 = 0, r₁ = 3

Solution

Problem 5 :

3x² - x + k = 0, r₁ = -5/3

Solution

Problem 6 :

Which graph has x-intercepts that are equivalent to the roots of the equation

(x - 3/2)²  = 25/4

Solution

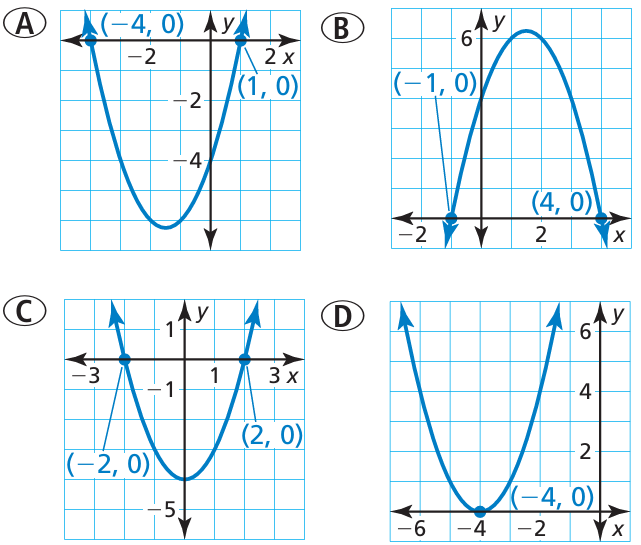
Problem 7 :

Write the quadratic function in the form f(x) = x² + bx + c that has zeroes 8 and 11

Solution