STAAR ALGEBRA 1 PRACTICE TEST WITH ANSWERS

Problem 1 :

Which answer choice describes how the graph of f(x) = x² was transformed to create the graph of n(x) = x² – 1 ?

A)  A vertical shift up        B)  A horizontal shift to the left

C)  A vertical shift down    D)  A horizontal shift to the right

Solution :

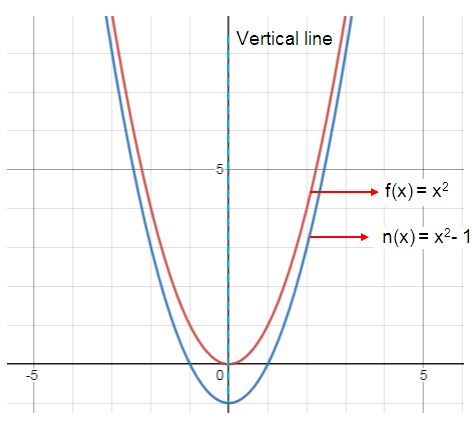
A vertical shift down.

So, option C) is correct.

Problem 2 :

The expression d² – d – 6 can be written in factored form as (d + 2) (d + k), where k represents a number. What is the value of k ? Record your answer and fill in the bubbles on your answer document.

Solution :

Given, the expression is d² – d – 6

Factored form of above quadratic function is,

(d - 3) (d + 2)

k = -3

So, the value of k is -3.

Problem 3 :

The graph of a linear function is shown on the grid.

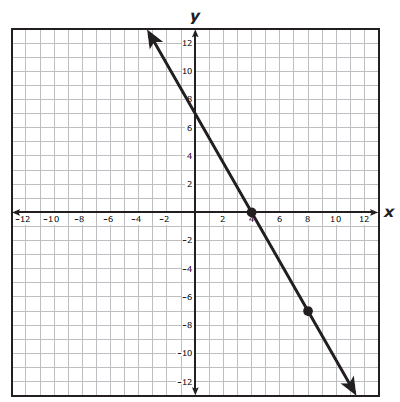
Which equation is best represented by this graph ?

Solution :

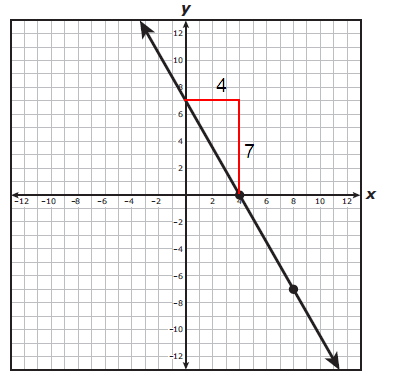
Slope (m) = -7/4

y - intercept (b) = 7

y = mx + b

y = -(7/4)x + 7 

So, option B) is correct.

Problem 4 :

Which expression is equivalent to (c⁸(d⁶)³)/c² for all values of c for which the expression is defined ?

F)  c⁴d⁹          G)  c⁴d¹⁸          H)  c⁶d⁹             J)  c⁶d¹⁸

Solution :

(c⁸(d⁶)³)/c²

(c⁸(d¹⁸))/c²

c⁶d¹⁸

So, option J) is correct.

Problem 5 :

Which value of x is the solution to this equation ?

5x² = 30x – 45

A)  x = 3         B)  x = -3         C)  x = 5        D)  x = -5

Solution :

5x² = 30x – 45

5x² - 30x + 45 = 0

a = 5, b = -30, c = 45

So, the value of x is 3.

Hence, option A) is correct.

Problem 6 :

A florist is making bouquets of flowers for a wedding. Each bouquet will have 9 flowers. The graph shows the linear relationship between y, the number of flowers used, and x, the number of bouquets.

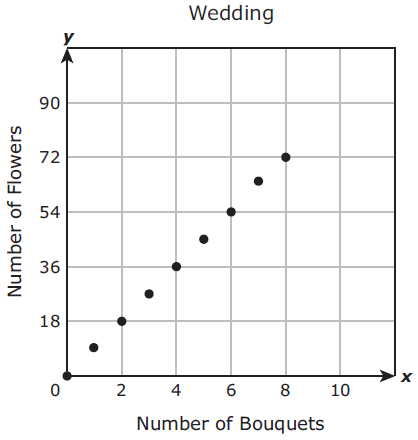
The florist will use no more than 8 bouquets for the wedding. Which set best represents the domain of the function for this situation ?

F) {0, 2, 4, 6, 8, 10}

G) {0, 1, 2, 3, 4, 5, 6, 7, 8}

H) {0, 18, 36, 54, 72, 90}

J) {0, 9, 18, 27, 36, 45, 54, 63, 72}

Solution :

Domain is all the possible x values of the function.

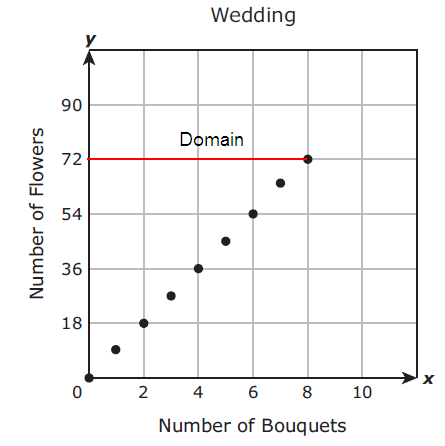
0 ≤ x ≤  8

{0, 1, 2, 3, 4, 5, 6, 7, 8}

So, option G) is correct.

Problem 7 :

The graph of a line is shown on the grid. The coordinates of both points indicated on the graph of the line are integers.

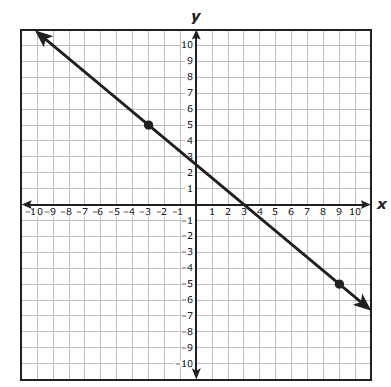
What is the rate of change of y with respect to x for this line ?

A) 5/2            B) -6/5          C) 2/3           D) -5/6

Solution :

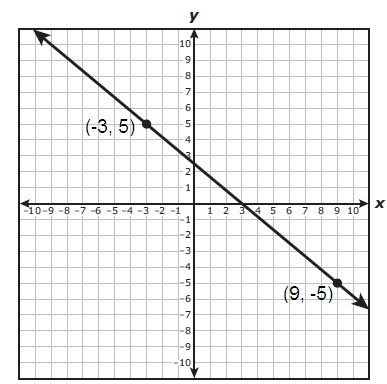
m = (y₂ - y₁)/(x₂ - x₁)

(x₁, y₁) = (-3, 5)

(x₂, y₂) = (9, -5)

m = (-5 - 5)/(9 + 3)

= -10/12

m = -5/6

So, option D) is correct.

Problem 8 :

What is the value of the y – intercept of the graph of h(x) = 12.3(4.9)^x ? Record your answer and fill in the bubbles on your answer document.

Solution :

h(x) = 12.3(4.9)^x

To find y - intercept :

x = 0

h(0) = 12.3(4.9)⁰

h(0) = 12.3

Problem 9 :

Which expression is equivalent to (8.8 × 10⁹)/(2.2 × 10^-3)

A) 4 × 10¹²     B) 4 × 10⁶        C) 4 × 10^-3           D) 4 × 10^-6

Solution :

8.8 = 4 × 2.2

= 4 × 10 ^{(9 + 3)}

= 4 × 10¹²

So, option A) is correct.

Problem 10 :

A person dives into a pool from its edge to swim to the other side. The table shows the depth in feet of the person from the surface of the water after x seconds. The data can be modeled by a quadratic function.

Pool

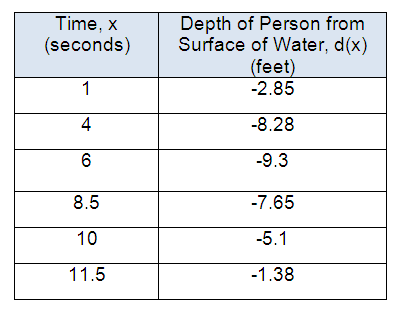
Which function best models the data ?

F) d(x) = 0.05x² + 0.74x

G) d(x) = 0.05x² + 0.74x + 9.17

H) d(x) = 0.26x² - 3.11x

J) d(x) = 0.26x² - 3.11x  + 1

Solution :

Quadratic function d(x) = ax² + bx + c

From the table, let us take first 3 values to get the equation.

x = 1 ==> y = -2.85

x = 4 ==> y = -8,28

x = 6 ==> y = -9.3

Now, the equations becomes,

a + b + c = -2.85 --- (1)

16a + 4b + c = -8.28 --- (2)

36a + 6b + c = -9.3 --- (3)

Solving (1) and (2) we get, 

-15a - 3b = 5.43

Dividing -3 on each sides.

5a + b = -1.81 --- (4)

Solving (3) and (1) we get, 

35a + 5b = -6.45

Dividing 5 on each sides.

7a + b = -0.52 --- (5)

Solving (4) and (5) we get, 

-2a  = -0.52

a = 0.52/2

a = 0.26

a = 0.26 substitute the equation (4).

5(0.26) + b = -1.81

1.3 = b = -1.81

b = -1.81 - 1.3

b = -3.11

a = 0.26 and b = -3.11 substitute the equation (1).

0.26 - 3.11 + c = -2.85

-2.85 + c = -2.85

c = -2.85 + 2.85

c = 0

a = 0.26, b = -3.11 and c = 0 substitute the quadratic function.

d(x) = 0.26x² - 3.11x 

So, option H) is correct.