SQUARE AND SQUARE ROOTS PRACTICE QUESTIONS

Problem 1 :

The value of √144 + √1.44 is ?

a. 24        b. 13.2       c. 1.32        d. none of these

Solution :

√144 + √1.44

√144 = √12 x 12

= 12

√1.44 = √1.44 x (100/100)

= √(144/100)

= √(12 x 12) /(10 x 10)

= 12/10

= 1.2

√144 + √1.44 = 12 + 1.2

= 13.2

Problem 2 :

Which of the following triplet is a Pythagorean Triplet:

a. (4, 5, 6)    b. (11, 60, 61)     c. (10, 8, 6)    d. both b and c

Solution :

Option a :

a = 4, b = 5 and c = 6

c² = a² + b²

6² = 4² + 5²

36 = 16 + 25

36 ≠ 41

So, option a is not Pythagorean triple.

Option b :

a = 11, b = 60 and c = 61

c² = a² + b²

61² = 11² + 60²

3721 = 121 + 3600

3721 = 3721

So, option b is Pythagorean triple.

Option c :

a = 10, b = 8 and c = 6

c² = a² + b²

10² = 8² + 6²

100 = 64 + 36

100 = 100

So, option c is Pythagorean triple.

Hence the correct answer is option d.

Problem 3 :

How many non square numbers are there in between 𝑛² 𝑎𝑛𝑑 (𝑛 + 1)²

a. 2n      b. 4n      c. 3n       d. 2n + 1

Solution :

There must be 2n natural numbers in between two consecutive numbers. So, the answer is option a.

Problem 4 :

The Simplified form of 

is

a. 30      b. 3     c. 10       d. None

Solution :

So, the answer is 10.

Problem 5 :

Evaluate √5² + 12²

Solution :

√5² + 12²

= √25 + 144

= √169

Problem 6 :

2707/√x = 27.07, find x.

Solution :

2707/√x = 27.07, find x.

Multiply by √x.

2707/√x = 27.07

Divide by 27.07 on both sides.

2707/27.07 = √x

100 = √x

Squaring both sides.

(100)² = x

x = 10000

So, the answer is 10000.

Problem 7 :

If √15625 = 125, then find the value of √156.25 + √1.5625

Solution :

√15625 = 125

= √156.25 + √1.5625

√156.25 + √1.5625 = 12.5 + 1.25

= 13.75

Problem 8 :

Find the square root of 14641 by prime factorisation method.

Solution :

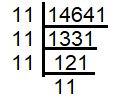
√14641 = √(11 x 11 x 11 x 11)

= 11 x 11

= 121

Problem 9 :

Find the square root of 144 by repeated subtraction method

Solution :

After 12 steps, we get 0. So, square root of 144 is 12.

Problem 10 :

Is 2352 a perfect square? If not, find the smallest multiple of 2352 which is a perfect square. Find the square root of the new number.

Solution :

Factoring 2352 :

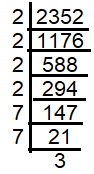
√2352 = √(2 x 2 x 2 x 2 x 7 x 7 x 3)

After grouping them as pairs, we find one 3 as extra. To group it, we need one more 3. So, 3 is the smallest number to be multiplied to make 2352 as perfect square.

Problem 11 :

Find the least number which should be subtracted from 180 to make it a perfect square.

Solution :

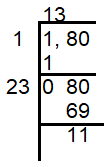
180 - 11 = 169

11 is the smallest number to be subtracted from 180 to make it as perfect square.

Problem 12 :

The length of a rectangle is 3 times its width. Its area is 972 sq. meter. Find the perimeter of the rectangle

Solution :

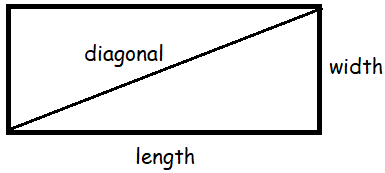
Let x be the width of the rectangle, then length will be 3x.

The diagonal will divide the rectangle into two identical triangles.

Area of triangle = area of rectangle / 2

= 972/2

= 486

(1/2) ⋅ 3x ⋅ x = 486

x² = (486 ⋅ 2)/3

x² = 324

x = √324

x = 18

3x = 3(18) ==> 54

Perimeter of rectangle = 2(length + width)

= 2(54 + 18)

= 2(72)

= 144 units.

Problem 13 :

A rectangle ABCD has AB = 12 cm and BC = 6 cm. Find the length of its diagonals correct to 2 decimal places.

Solution :

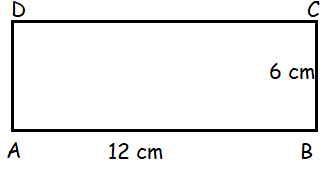
AC² = AB² + BC²

AC² = 12² + 6²

= 144 + 36

= 180

AC = √180

AC = 13.41

So, the length of the diagnal is 13.41 cm

Problem 14 :

Find the number of non-square numbers lying between 40² and 41².

a) 80     b) 40   c) 30     d) 84

Solution :

In between n² and (n + 1)², we will have 2n non square numbers.

When n = 40, n + 1 = 41

2n = 2(40)

= 80 non square numbers.

Problem 15 :

If m, n, p are natural numbers such that (m, n, p) forms a Pythagorean triplet if ?

a) m² + n² = p²      b) m² + n² < p²    d) m² + n² ≠ p

Solution :

(m, n, p) forms a Pythagorean triplet.

m² + n² = p² 

Problem 16 :

The square of an even number is always____________.

a) even     b) odd     c)  may be even or odd      d)  none

Solution :

• Let the even number as 4, its square = 4² ==> 16
• Let the even number as 6, its square = 6² ==> 36

So, square of even number is also an even number. Option a is correct.

Problem 17 :

The square root of 0.09 + 2 x 0.21 + 0.49 is

a) √0.09 + √0.49     b) 2 √0.21     c) 1     d) 0.58

Solution :

= √(0.09 + 2 x 0.21 + 0.49)

= √(0.3)² + 2 x (0.3)(0.7) + (0.7)²

= √(0.3 + 0.7)²

= √1²

= 1

So, option c is correct.

Problem 18 :

The digit in the unit’s place in the square root of 15876 is

a) 8     b)  6       c)  4    d)  2

Solution :

= √(2 x 2 x 3 x 3 x 3 x 7 x 7 x 3)

= 2 x 3 x 3 x 7

= 126

So, the unit digit is 6.