SPECIAL RIGHT TRIANGLE PROBLEMS SAT

Problem 1 :

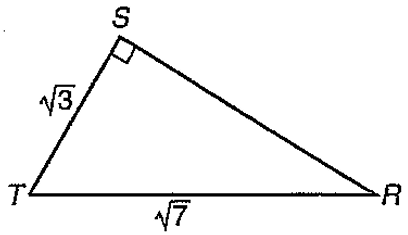
In the figure above, what is the length of RS ?

a)  √7 - √3       b)  2      c)  4      d)  7 + √3      e)  10

Solution :

In the right triangle,

TR² = TS² + SR²

√7² = √3² + SR²

7 = 3 + SR²

SR² = 7 - 3

SR² = 4

SR = √4

SR = 2

So, the measure of RS is 2.

Problem 2 :

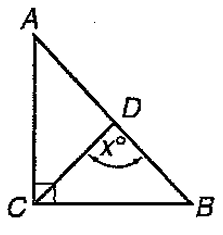
In triangle ABC, ∠C = 90, CD = BD and the ratio of the measure of ∠A to the measure of ∠B is 2 to 3. What is the value of x ?

a)  18    b)  36     c)  40     d)  54    e)  72

Solution :

In the right triangle ABC,

∠A : ∠B = 2 : 3

∠A = 2x and ∠B = 3x

∠A  + ∠B + ∠C = 180

2x + 3x + 90 = 180

5x = 180 - 90

5x = 90

x = 90/5

x = 18

∠DBC = ∠DCB

3x = ∠DCB

3(18) = ∠DCB

∠DCB = 54

In triangle DCB,

∠DCB + ∠DBC + ∠CDB = 180

54 + 54 + ∠CDB = 180

108 + ∠CDB = 180

∠CDB = 180 - 108

∠CDB = 72

So, the value of x is 72. Option e is correct.

Problem 3 :

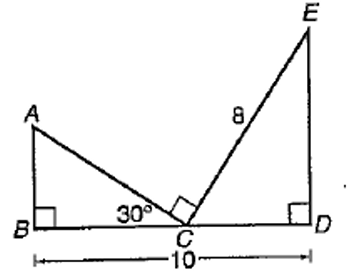
In the figure given above, what is the length of the line segment AB ?

a)  3       b)  2√3      c)  4       d)  3√3      e) 6

Solution :

∠BCA + ∠ACE + ∠ECD = 180

30 + 90 + ∠ECD = 180

120 + ∠ECD = 180

∠ECD = 180 - 120

∠ECD = 60

Let BC = x, then CD = 10 - x

In triangle CED,

CE = hypotenuse = 8

Hypotenuse = 2(smaller side)

2 (10 - x) = 8

10 - x = 8/2

10 - x = 4

x = 10 - 4

x = 6

BC = x = 6

√3 smaller side = the side which is opposie to 60 degree

BC = √3AB

6 = √3AB

AB = 6/√3

AB = (6/√3) ⋅ (√3/√3)

= 6√3/3

AB = 2√3

So, option b is correct.

Problem 4 :

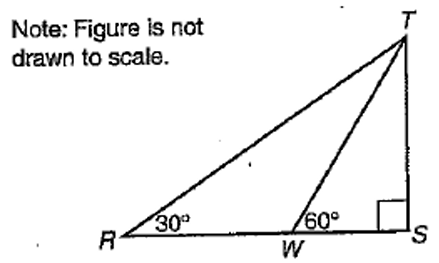
In the figure given above, what is the ratio of RW to WS ?

a)  √2 to 1      b)  √3 to 1      c)  2 to 1     d)  3 to 1     e)  3 to 2

Solution :

In triangle TRS,

∠RTS = 180 - (30 + 90)

= 180 - 120

= 60

Let WS = x (the smaller side)

RS = √3x

RW = RS - WS

= √3x - x

RW = (√3 - 1)x

RW : WS = (√3 - 1) x  : x

= (√3 - 1) : 1 

So, option c is correct.

Problem 5 :

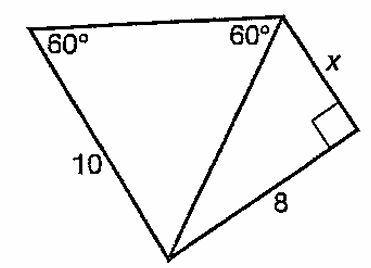
In the figure above, x = ?

a)  4    b)  6   c)  4√2      d)  4√3   e)  8√3

Solution :

In the 30-60-90 right triangle,

Hypontenuse = 10

Using Pythagorean theorem,

10² = 8² + x²

100 = 64 + x²

x² = 100 - 64

x² = 36

x = 6

So, option b is correct.

Problem 6 :

Find 𝐴𝐶 if ∠𝐴 = 30°, ∠𝐷 = 45°, and 𝐵𝐷 = 8.

Solution :

In triangle ABC,

∠𝐴 = 30°, ∠C = 90°, ∠ABC = 60°

In triangle BCD,

∠D = 45°, ∠C = 90°, ∠DBC = 45°

Let CD = x = BC

BD² = BC² + CD²

8² = x² + x²

2x² = 64

x² = 64/2

x² = 32

x = √32

= √(2 x 2 x 2 x 2 x 2)

x = 4√2 = CD = BC

BC is the side which is opposite to 30 degree. Then the measure which is opposite to 60 degree will be √3(4√2)

AC = 4√6

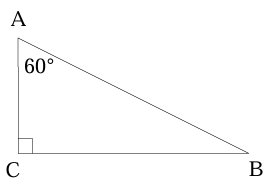
Problem 7 :

Given: Right ∆𝐴𝐵𝐶 with ∠𝐶 = 90° and ∠𝐴 = 60°; 𝐴𝐵 = 20. Find: 𝐵𝐶

Solution :

AB = hypotenuse

BC = the side which is opposite to 60 degree

AC = the side which is opposite to 30 degree and smaller side

2AC = AB

2AC = 20

AC = 20/2

AC = 10

BC = √3(AC)

= 10√3

So, the length of BC is 10√3.

Problem 8 :

In the figure above, if AD = BD = 2√3, what is the length of AB ?

a)  4√3        b)  3√6       c)  6       d)  6√2

Solution :

Triangle ABC is a 30-60-90 speical right triangle. ∠CDA = 60 degree and ∠CAD = 30

Triangle ACD is also an 30-60-90 special right triangle.

AD = 2(CD)

2√3 = 2CD

CD = √3

AC = √3(CD)

= √3(√3)

= 3

CD + DB = √3 + 2√3

BC = 3√3

AC² + BC² = AB²

3² + (3√3)² = AB²

9 + 9(3) = AB²

AB² = 9 + 27

AB² = 36

AB = 6

So, option c is correct.

Problem 9 :

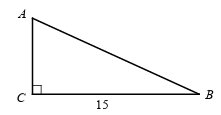
In the figure above, the area of right triangle ABC is 60. What is the perimeter of ABC?

a) 34             b) 36           c) 38             d) 40

Solution :

Area of right triangle = (1/2) x base x height

base = 15 and height = h

60 = (1/2) x 15 x h

60(2) / 15 = h

h = 120/15

h = 8

AC² + BC² = AB²

8² + 15² = AB²

64 + 225 = AB²

AB² = 289

AB = √289

AB = 17

Problem 10 :

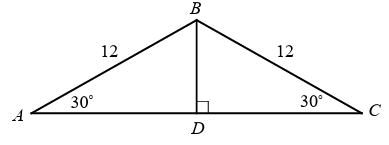
In the figure above, what is the area of ABC?

a) 24√3     b) 30√3      c) 36√3      d) 48√3

∠ABD = 60 and ∠DBC = 60

AB = 2(BD)

12 = 2(BD)

BD = 12/2

BD = 6

AD² + BD² = AB²

AD² + 6² = 12²

AD² = 144 - 36

AD² = 108

AD = √108

= √(3 x 6 x 6)

AD = 6√3

AC = 2(AD)

= 2(6√3)

= 12√3

Area of triangle = (1/2) x 12√3 x 6

= 36√3

So, option c is correct.