SOLVING WORD PROBLEMS WITH DIAGONALS OF 2D SHAPES

Problem 1 :

Find the diagonal of a square whose perimeter is 60 cm.

Solution :

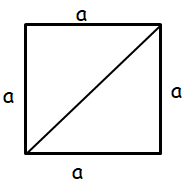
4a = 60

a = 60/4 ==> 15

Square of diagonal = sum of squares of remaining sides

a² + a² = (diagonal)²

(diagonal)² = 15² + 15²

(diagonal)² = 225 + 225

(diagonal)² = 450

diagonal = √450

diagonal = √3 x 3 x 5 x 5 x 2

= (3 x 5)√2

= 15√2

So, the length of diagonal of the square is 15√2.

Problem 2 :

Perimeter of a rhombus is 146 cm and the length of one of its diagonals is 48 cm. Find the length of its other diagonal.

Solution :

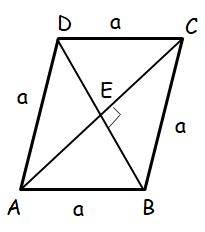
AC = 48 cm, DB = x

AE = EC = 24 cm and EB = x/2 cm

Perimeter of rhombus = 146 cm

4a = 146

a = 146/4

a = 36.5

In triangle AEB,

AB² = AE² + EB²

(36.5)² = 24² + (x/2)²

1332.25 = 576 + (x² / 4)

1332.25 - 576 = (x² / 4)

4 (756.25) = x²

x = √4 (756.25)

x = 55 cm

DB = 55 cm

So, the length of the other diagonal is 55 cm.

Problem 3 :

If diagonal of one square is double the diagonal of another square, then find the ratio of their areas.

Solution :

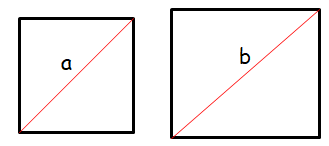
b = 2a

Side length of small square = a/√2

Side length of large square = b/√2

Area of square = (side)²

(a/√2)² : (b/√2)²

(a/√2)² : (2a/√2)²

(a² / 2) : (4a² / 2)

a² : 4a²

1 : 4

So, the required ratio is 1 : 4

Problem 4 :

If diagonal of a rectangle is thrice its smaller side, then find the ratio of its length and width.

Solution :

Length be the longer side and width be the smaller side

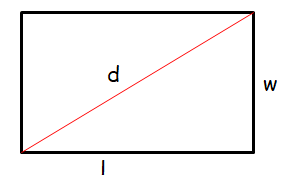
d = 3w

Using Pythagorean theorem,

l² + w² = d²

l² + w² = (3w)²

l² + w² = 9w²

l² = 9w² - w²

l² = 8w²

l²/w² = 8/1

(l/w)² = 8/1

(l/w) = √(8/1)

l : w = 2√2 : 1

Problem 5 :

A rectangular carpet has area 120 square meters and perimeter 46 meters. The length of its diagonal is ____

Solution :

Area of rectangle = 120 square meter

Let l and w be the length and width of rectangle.

l w = 120 ------(1)

perimeter of the rectangle = 46 meter

2(l + w) = 46

l + w = 46/2

l + w = 23 ------(2)

120 = 15 x 8

l = 15 cm and w = 8 cm

d² = l² + w²

d² = 15² + 8²

d² = 225 + 64

d² = 289

d = 17 cm

So, the length of the diagonal is 17 cm.

Problem 6 :

If length of diagonal of a square is 20 cm, then its perimeter is _______

Solution :

Length of the diagonal of square = 20 cm

Let x be the side length of square

x² + x² = 20²

2x² = 400

x² = 200

x = √200

x = √2 x 10 x 10

x = 10 √2

Perimeter of square = 4 x side length

= 4 (10 √2)

= 40√2 cm

Problem 7 :

A square dinner napkin 8 in. on each side is folded along its diagonal. Find the area of the folder napkin.

Solution :

Length of the diagonal of square = 8 in

Let x be the length of diagonal.

The diagonal will divide the square into two right triangles.

Using Pythagorean theorem, 

x² + x² = 8²

2x² = 64

x² = 64/2

x² = 32

x = √32

x = 4√2 cm

Area of square = 32 square cm.

Problem 8 :

What is the area of the rhombus ABCD, if AC = 6 cm, and BE = 4 cm?

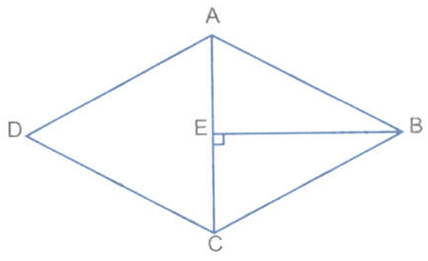
Solution :

The diagonal of rhombus will bisect each other at right angles.

AC = 6 cm, AE = 3 cm

In right triangle AEB,

AE² + EB² = AB²

3² + 4² = AB²

9 + 16 = AB²

AB² = 25

AB = 5 cm

Length of one diagonal = BD = 8 cm

Length of other diagonal = AC = 6 cm

Area of rhombus = (1/2) product of diagonals

= (1/2) x 8 x 6

= 24 cm²