SOLVING WORD PROBLEMS USING SQUARE ROOTS

Problem 1 :

A school collected $2304 as fees from its students. If each student paid as many dollars as there were students in the school, how many students were there in the school?

Solution :

Let x be the number of students in the school. Amount of denomination by each student = x.

x ⋅ x = 2304

x² = 2304

x = √2304

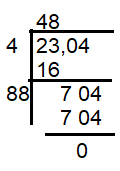
Number of students in the school = 48

Amount of denomination by each student = $48

Problem 2 :

2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.

Solution :

Let x be the number of rows. Number of plants in each row is x.

Number of rows ⋅ number of plants in each row = x ⋅ x

x ⋅ x = 2025

x² = 2025

x = √2025

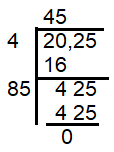
So, number of rows is 45 and number of plants in each row is also 45.

Problem 3 :

10404 students are sitting in a lecture room in such a manner that there are as many students in a row as there are rows in a lecture room. How many students are there in each row of a lecture room?

Solution :

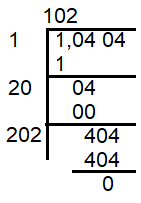
So, in each row there are 102 students.

Problem 4 :

Find the smallest number by which 1800 must be multiplied so that it becomes a perfect square. Also find the square root of the perfect square so obtained.

Solution :

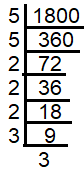
1800 = 5 x 5 x 2 x 2 x 2 x 3 x 3

After grouping them as pairs, we see one 2 is insufficient. So, 2 is the number to be multiplied to make it is as perfect square. Multiplying 2 on both sides, we get

1800 x 2 = 5 x 5 x 2 x 2 x 2 x 3 x 3 x 2

3600

Taking square root on both sides,

√3600 = √(5 x 5 x 2 x 2 x 2 x 3 x 3 x 2)

= 60

So, the square root of the number obtained is 60.

Problem 5 :

Is 2352 a perfect square? if not, find the smallest number by which 2352 must be multiplied so that the product is a perfect square. Find the square root of new number.

Solution :

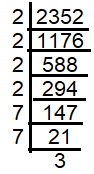
2352 = 2 x 2 x 2 x 2 x 7 x 7 x 3

After grouping them as pairs, we know that 2352 is not a perfect square, to make it as perfect square we need one 3 extra. 

By multiplying the old number by 3, we get = 7056

Square root of new number = √7056

= √(2 x 2) x (2 x 2) x (7 x 7) x (3 x 3)

= 2 x 2 x 7 x 3

= 84

Square root of the new number is 84.

Problem 6 :

The area of a square field is 8281 m². Find the length of its side.

Solution :

Area of square = 8281 m²

side x side = 8281 m²

side length = √8281

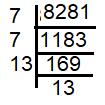
= √(7 x 7 x 13 x 13)

= 7 x 13

= 91

So, side length of square is 91 m.