SOLVING SIMPLE CUBIC EQUATIONS WORKSHEET

To solve cubic equation, we should know the inverse operation of cube.

To remove cube or raised to the power of 3, we have to take cube root on both sides.

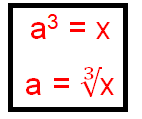
Step 1 :

Using inverse operations isolate the terms which has the highest exponent 3 in one side of the equal sign.

Step 2 :

After isolating the terms which has the highest exponent 3, to remove cube we will take cube root on both side of the equal sign.

Step 3 :

Decomposing the numerical value that we have inside the cube root as product of prime factors, for every three same values inside the cube root, take one value out of the radical sign.

Solve for x :

Problem 1 :

x³ = 64

Solution :

x³ = 64

x = ∛64

x = 4

Problem 2 :

x³ - 27 = 0

Solution :

x³ - 27 = 0

x³ = 27

x = ∛27

x = 3

Problem 3 :

x³ + 216 = 0

Solution :

x³ + 216 = 0

x³ = -216

x = ∛-216

x = -6

Problem 4 :

x³ = 0

Solution :

x³ = 0

x = 0

Problem 5 :

x³ = -125

Solution :

x³ = -125

x = ∛25

x = -5

Problem 6 :

x³ + 8 = 0

Solution :

x³ + 8 = 0

x³ = -8

x = ∛-8

x = -2

Problem 7 :

x³ - 1 = 0

Solution :

x³ - 1 = 0

x³ = 1

x = ∛1

x = 1

Problem 8 :

x³ = -1000000

Solution :

x³ = -1000000

x = ∛-1000000

x = -100

Problem 9 :

x³ = 512

Solution :

x³ = 512

x = ∛512

x = 8

Problem 10 :

x³ + 1 = 0

Solution :

x³ + 1 = 0

x³ = -1

x = ∛-1

x = -1

Problem 11 :

Solve 2x³ − 12x² + 18x = 0

Solution :

2x³ − 12x² + 18x = 0

Factoring 2x, we get

2x(x² − 6x + 9) = 0

2x(x² − 3x - 3x + 9) = 0

2x[x(x - 3) - 3(x - 3)] = 0

2x(x - 3)(x - 3) = 0

Equating each factor equal to 0, we get

2x = 0 and x - 3 = 0

x = 0 and x = 3

So, the solutions are 0, 3 and 3.

Problem 12 :

Solve 36x³ − x = 0

Solution :

36x³ − x = 0

Factoring x, we get

x(36x² − 1) = 0

x(6²x² − 1²) = 0

x[(6x)² − 1²] = 0

x(6x - 1)(6x + 1) = 0

Equating each factor to 0, we get

x = 0, 6x + 1 = 0, 6x - 1 = 0

So, the solutions are -1/6, 0 and 1/6.

Problem 13 :

Solve 20x³ + 80x² = -60x

Solution :

20x³ + 80x² = -60x

20x³ + 80x² + 60x = 0

Factoring 20x, we get

20x(x² + 4x + 3) = 0

20x(x² + 1x + 3x + 3) = 0

20x[x (x + 1) + 3(x + 1)] = 0

20x (x + 1) (x + 3) = 0

Equating each factor to 0, we get

The solutions are -3, -1 and 0.

Problem 14 :

Solve 3x² = 75x⁴

Solution :

3x² = 75x⁴

x² = 25x⁴

25x⁴ - x² = 0

Factoring x², we get

x² (25x² - 1) = 0

x² (5²x² - 1) = 0

x² ((5x)² - 1²) = 0

x² (5x + 1)(5x - 1) = 0

Equating each factor equal to 0, we get

So, values of x are -1/5, 0 and 1/5.

Problem 15 :

-13x² + 36 = -x⁴

Solution :

-13x² + 36 = -x⁴

x⁴ - 13x² + 36 = 0

Let t = x²

(x²)² - 13t + 36 = 0

t² - 13t + 36 = 0

t² - 13t + 36 = 0

t² - 9t - 4t + 36 = 0

t(t - 9) - 4(t - 9) = 0

(t - 4)(t - 9) = 0

Equating each factor to 0, we get

t = 4 and t = 9

So, the solutions are 4, 4, 9 and 9.

Problem 16 :

2x³ - x² - 2x = -1

Solution :

2x³ - x² - 2x = -1

2x³ - x² - 2x + 1 = 0

Factoring x² from the first two terms and negative from last two terms, we get

x²(2x - 1) - 1(2x - 1) = 0

(x² - 1) (2x - 1) = 0

(x + 1)(x - 1) (2x - 1) = 0

x = -1, x = 1 and x = 1/2

So, the solutions are -1, 1/2 and 1.