SOLVING RADICAL EQUATIONS WITH SQUARE ROOTS

Solve for x :

Example 1 :

5√2 = √x

Solution :

To remove the square root, we can take squares on both sides.

(5√2)² = (√x)²

Distributing the power for all the terms that we have in the power.

5²√2² = (√x)²

25 (2) = x

x = 50

Example 2 :

3√x = √45

Solution :

To remove the square root, we can take squares on both sides.

(3√x)² = (√45)²

Distributing the power for all the terms that we have in the power.

3²√x² = (√45)²

9x = 45

Divide by 9 on both sides.

x = 45/9

x = 5

Example 3 :

2√2 = √4x

Solution :

To remove the square root, we can take squares on both sides.

(2√2)² = (√4x)²

Distributing the power for all the terms that we have in the power.

2²√2² = (√4x)²

4(2) = 4x

Divide by 4 on both sides.

x = 8/4

x = 2

Example 4 :

√(x + 1) = 6

what value of x satisfies the equation above ?

(a) 5   (b) 6   (c)  35   (d)  36

Solution :

√(x + 1) = 6

Taking squares on both sides.

x + 1 = 6²

x + 1 = 36

Subtracting 1 on both sides.

x = 36 - 1

x = 35

Example 5 :

(x - 12) = √(x + 44)

What are all possible solution to the given equation ?

(a)  5   (b)  20   (c)  -5 and 20   (d)  5 and 20

Solution :

(x - 12) = √(x + 44)

Take squares on both sides.

(x - 12)² = (x + 44)

Using the algebraic identity,

(a - b)² = a² - 2ab + b²

x² - 2x(12) + 12² = x + 44

x² - 24x + 144 = x + 44

Subtract x and 44 on both sides.

x²-25x+100 = 0

(x-20)(x-5) = 0

Equating each factor to zero, we get

x = 20 and x = 5

Example 6 :

x + 3√x = 28

Solution :

x + 3√x = 28

Subtract x on both sides.

3√x = 28 - x

Take squares on both sides.

(3√x)² = (28 - x)²

9x = 784 - 56x + x²

By subtracting 9x on both sides.

x² - 65x+784 = 0

(x-49)(x-16) = 0

x = 49 and x = 16

Example 7 :

Solve for x, 3/x = √0.09

Solution :

3/x = √0.09

3/x = √(9/100)

3/x = √(3 x 3/10 x 10)

3/x = 3/10

Doing cross multiplication, we get

3(10) = 3x

x = 30/3

x = 10

So, the value of x is 10.

Example 8 :

A Shell station stores its gasoline in underground tanks that are right circular cylinders lying on their sides.See the illustration. The volume V of gasoline in the tank (in gallons) is given by the formula

V = 40h²√(96/h) - 0.608

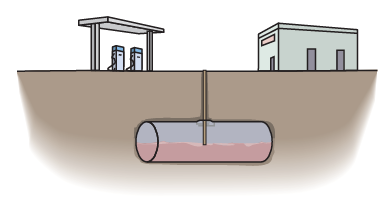
where h is the height of the gasoline (in inches) as measured on a depth stick.

(a) If h = 12 inches, how many gallons of gasoline are in the tank?

(b) If h = 1 inch, how many gallons of gasoline are in the tank?

Solution :

(a) When h = 12

V = 40(12)²√(96/12) - 0.608

= 40(144) √(8 - 0.608)

= 40(144) √7.392

= 5760 (2.71)

= 15660 gallons

(a) When h = 1

V = 40(1)²√(96/1) - 0.608

= 40 √(96 - 0.608)

= 40√95.392

= 40(9.76)

= 390.6 gallons

Example 9 :

Solve √(3 - 2√x)) = √x

Solution :

√(3 - 2√x)) = √x

Squaring on both sides

(3 - 2√x)) = (√x)²

3 - 2√x = x

3 - x =  2√x

Squaring on both sides, we get

(3 - x)² =  (2√x)²

9 - 6x + x²  = 4x

x²  + 4x + 6x - 9 = 0

x²  + 10x  - 9 = 0

Example 10 :

If c = 3√5 and 5c = √5z, what is the value of z ?

Solution :

c = 3√5 and 5c = √5z

Applying the value of c, we get

5(3√5) = √5z

Squaring both sides, we get

[5(3√5)]² = [√5z]²

25(9) (5) = 5z

z = 125 (9)/5

z = 25(9)

= 225

So, the value of z is 225.

Example 11 :

In the equation y - √(4x² + 28) = 0, x > 0 and y = 8. What is the value of x ?

Solution :

y - √(4x² + 28) = 0

y = √(4x² + 28)

Applying y = 8, we get

8 = √(4x² + 28)

64 = 4x² + 28

64 - 28 = 4x²

4x² = 36

x² = 36/4

x² = 9

x = ±3

x = -3 and x = 3

Since x > 0, then we choose 3.

Example 12 :

If k = 1, which of the following is the solution set for x - 7 = √(x - k) ?

Solution :

x - 7 = √(x - k)

Given that k = 1, we get

x - 7 = √(x - 1)

Squaring on both sides, we get

(x - 7)² = (√(x - 1))²

x² - 14x + 49 = x - 1

x² - 14x - x + 49 + 1 = 0

x² - 15x + 50 = 0

(x - 10)(x - 5) = 0

x = 10 and x = 5