SOLVING QUADRATIC INEQUALITIES WORD PROBLEMS

Solve for the following quadratic inequalities.

Example 1 :

Given 𝐴 = 𝑥² − 7 and 𝐵 = −4𝑥 + 5, for what values of 𝑥 is 𝐴 < 𝐵?

Solution :

𝐴 = 𝑥² − 7 and 𝐵 = −4𝑥 + 5

Given that A < B

𝑥² − 7 < -4x + 5

𝑥² + 4x − 7 - 5 < 0

𝑥² + 4x − 12 < 0

𝑥² + 6x - 2x - 12 < 0

Finding critical numbers :

x(x + 6) - 2(x + 6) =  0

(x - 2)(x + 6) < 0

x = 2 and x = -6

Converting into intervals :

(-∞, -6) (-6, 2) and (2, ∞)

When x ∈ (2, ∞)

f(x) < 0

When x = 3

= (3 - 2)(3 + 6)

= 1(9)

= 9 < 0 (False)

So, the solution is (-6, 2).

Example 2 :

When a projectile is fired into the air, its height h, in meters, t seconds later is given by the equation ℎ(𝑡) = 11𝑡 − 3𝑡². When is the projectile at least 6 m above the ground?

Solution :

Given that ℎ(𝑡) = 11𝑡 − 3𝑡²

At least 6 m above the ground, then

11𝑡 − 3𝑡² > 6

− 3𝑡² + 11t - 6 > 0

Multiplying by negative, we get 

3𝑡² - 11t + 6 < 0

3𝑡² - 9t - 2t + 6 < 0

3t(t - 3) - 2(t - 3) < 0

(3t - 2) (t - 3) < 0

Finding critical numbers :

3t - 2 = 0 and t - 3 = 0

t = 2/3 and y = 3

(-∞, 2/3) (2/3, 3) and (3, ∞)

When x ∈ (3, ∞)

x = 4

(3t - 2) (t - 3) < 0

(3(4) - 2) (4 - 3) < 0

6(1) < 0

6 < 0

False

So, the solution is (2/3, 3). The possible values of x are 2/3 < x < 3.

Example 3 :

The arch of the Sydney Harbor Bridge in Sydney, Australia, can be modeled by

y = −0.00211x² + 1.06x

where x is the distance (in meters) from the left pylons and y is the height (in meters) of the arch above the water. For what distances x is the arch above the road?

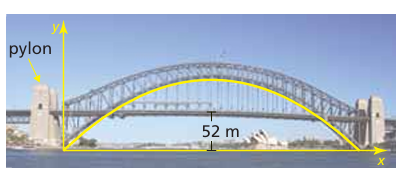
Solution :

y = −0.00211x² + 1.06x

−0.00211x² + 1.06x > 52

−0.00211x² + 1.06x - 52 > 0

multiplying by negative sign, we get

0.00211x² - 1.06x + 52 > 0

a = 0.00211, b = -1.06 and c = 52

x = [-b + √(b² - 4ac)]/2a

= [-(-1.06) ± √(-1.06)² - 4(0.00211)(52)] / 2(0.00211)

= [1.06 ± √(1.1236 - 0.43888)] / 0.00422

= [1.06 ± √0.68472] / 0.00422

= [1.06 ± 0.8274] / 0.00422

= (1.06 + 0.8274) / 0.00422 and (1.06 - 0.8274) / 0.00422

= 1.8874/0.00422 and 0.2326 / 0.00422

= 447.25 and 55.11

Since the arch is above the road for distances between the roots, the answer is

55.11 < x < 447.25

Example 4 :

The number T of teams that have participated in a robot-building competition for high-school students over a recent period of time x (in years) can be modeled by

T(x) = 17.155 x² + 193.68 x + 235.81, 0 ≤ x ≤ 6.

After how many years is the number of teams greater than 1000? Justify your answer.

Solution :

T(x) = 17.155 x² + 193.68 x + 235.81

Number of teams greater than 1000

17.155 x² + 193.68 x + 235.81 > 1000

17.155 x² + 193.68 x + 235.81 - 1000 > 0

17.155 x² + 193.68 x - 764.19 > 0

a = 17.155, b = 193.68 and c = -764.19

x = [-b + √(b² - 4ac)]/2a

= [-193.68 ± √(193.68)² - 4(17.155)(-764.19)] / 2(17.155)

= [-193.68 ± √(37511.94 + 52438)] / 34.31

= [-193.68 ± √(89949.94)] / 34.31

= [-193.68 ± √(89949.94)] / 34.31

= [-193.68 ± 299.9] / 34.31

= [-193.68 + 300] / 34.31, [-193.68 - 300] / 34.31

x = 106.32/34.31, 493.68/34.31

x = 3.09

Example 5 :

A rectangular fountain display has a perimeter of 400 feet and an area of at least 9100 feet. Describe the possible widths of the fountain.

Solution :

Let x and y be the length and width of the rectangle.

Perimeter of rectangle = 400 feet

2(x + y) = 400

x + y = 200

y = 200 - x -----(1)

Area of rectangle at least 9100

xy > 9100

x(200 - x) > 9100

200x - x² > 9100

- x² + 200 x > 9100

- x² + 200 x - 9100 > 0

Multiplying by negative, we get

 x² - 200 x + 9100 > 0

 x² - 130x - 70x + 9100 > 0

x(x - 130) - 70(x - 130) > 0

(x - 130)(x - 70) > 0

Finding critical numbers :

x - 130 = 0 and x - 70 = 0

x = 130 and x = 70

 (-∞, 70) (70, 130) and (130, ∞)

When x ∈ (130, ∞)

x = 140

(x - 130)(x - 70) > 0

(140 - 130)(140 - 70) > 0

10(70) > 0

700 > 0

True

The possible solutions are  (-∞, 70) and (130, ∞).