SOLVING QUADRATIC EQUATIONS

To solve a quadratic equation which is in the form

ax² + bx + c = 0

we have three different ways.

(i) Factoring

(ii) Quadratic formula

(iii) Completing the square

Solving Quadratic Equations by Factoring

Problem 1 :

x² - 4x + 3 = 0

Solution :

x² - 4x + 3 = 0

Since the coefficient of x² is 1, we take the constant alone and decompose it into two parts.

Factors of 3 :

The middle term alone is negative, so both factors will be negative.

x² - x - 3x + 3 = 0

x(x - 1) - 3(x - 1) = 0

(x - 1) (x - 3) = 0

x = 1 and x = 3

So, the solution is {1, 3}.

Problem 2 :

2x² - x = 12 + x

Solution : 

2x² - x = 12 + x

The given question is not in the standard form, so subtract 12 and x to get rid of it.

2x² - x - x - 12 = 0

2x² - 2x - 12 = 0

2(x² - x - 6) = 0

2(x² + 2x - 3x - 6) = 0

2(x + 2) (x - 3) = 0

(x + 2) (x - 3) = 0

x = -2 and x = 3

So, the solution is {-2, 3}.

Solving Quadratic Equation by Formula 

Problem 3 :

Solve

2x² + x - 4 = 0

Solution :

Problem 4 :

Using completing the square method, solve the equation.

x² − 6x − 7 = 0

Solution :

x² − 2⋅x⋅3 + 3² - 3² - 7 = 0

Write the coefficient of x as a multiple of 2.

(x - 3)² - 3² - 7 = 0

(x - 3)² - 9 - 7 = 0

(x - 3)² - 16 = 0

Add 16 on both sides.

(x - 3)² = 16

Take square roots on both sides, we get

x - 3 = √16

x - 3 =  ±4

x - 3 = 4 and x - 3 = -4

x = 4 + 3 and x = - 4 + 3

x = 7 and x = -1

Solving Quadratic Equations in Different Forms

Problem 5 :

3(x + 7)² + 17 = 56

Solution :

The given question is not in the standard form.

3(x + 7)² + 17 = 56

Subtract 17 on both sides.

3(x + 7)² + 17 - 17 = 56 - 17

3(x + 7)² = 39

Divide by 3 on both sides.

(x + 7)² = 39/3

(x + 7)² = 13

(x + 7) = √13

x + 7 = ±√13

x = ±√13 - 7

Problem 6 :

2x - 5√x + 2 = 0

Solution :

It is trinomial, even though it doesn't have square, by considering the middle term (√x). Let us try to write the other terms also in terms of √x.

2(√x)² - 5√x + 2 = 0

Let √x = t

2t² - 5t + 2 = 0

2t² - 4t - 1t + 2 = 0

2t(t - 2) - 1(t - 2) = 0

(2t - 1) (t - 2) = 0

Equating each factor to 0, we get

t = 1/2 and t = 2

When t = 1/2 ==>  √x = 1/2 ==> x = 1/4

When t = 2 ==>  √x = 2 ==> x = 4

Problem 7 :

The height y (in yards) of a flop shot in golf can be modeled by

y = −x² + 5x

where x is the horizontal distance (in yards).

a. Interpret the x-intercepts of the graph of the equation.

b. How far away does the golf ball land ?

Solution :

y = −x² + 5x

a) To find x-intercept, we have to put y = 0

−x² + 5x = 0

-x(x - 5) = 0

x = 0 and x = 5

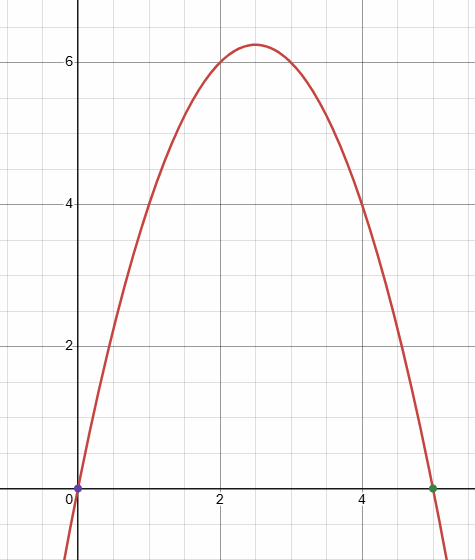
b)  The horizontal distance covered by the ball is 5 yards.

Problem 8 :

The height h (in feet) of an underhand volleyball serve can be modeled by

h = −16t² + 30t + 4

where t is the time (in seconds).

a. Do both t-intercepts of the graph of the function have meaning in this situation? Explain.

b. No one receives the serve. After how many seconds does the volleyball hit the ground?

Solution :

h = −16t² + 30t + 4

0 = −16t² + 30t + 4

−16t² + 30t + 4 = 0

−16t² + 32t - 2t + 4 = 0

-16t(t - 2) - 2(t - 2) = 0

(t - 2)(-16t - 2) = 0

t = 2 and t = -2/16

t = -1/8

a) The positive value alone will give meaning.

b)  After 2 seconds the volley ball hit the ground.

Problem 9 :

At a Civil War reenactment, a cannonball is fi red into the air with an initial vertical velocity of 128 feet per second. The release point is 6 feet above the ground. The function

h = −16t² + 128t + 6

represents the height h (in feet) of the cannonball after t seconds. 

a. Find the maximum height of the cannonball after it is fired.

b. Use the results of part (a) to estimate when the height of the cannonball is 150 feet.

Solution :

h = −16t² + 128t + 6

a)  The maximum height reached by the ball

x = -b/2a

a = -16, b = 128 and c = 6

t = -128/2(-16)

t = 128/32

t = 4

After 4 seconds it is fired, it reaches the maximum height.

When t = 4

h = −16(4)² + 128(4) + 6

= -16(16) + 512 + 6

= -256 + 512 + 6

= 262 ft

b)  When h = 150 ft

−16t² + 128t + 6 = 150

−16t² + 128t + 6 - 150 = 0

−16t² + 128t - 144 = 0

-16(t² - 8t + 9) = 0

t² - 8t + 9 = 0

= (-b ± √b² - 4ac)/2a

= (8 ± √8² - 36)/2

= (8 ± √(64 - 36))/2

= (8 ± √28)/2

= (8 + 5.29)/2, (8 - 5.29)/2

= 13.29/2, 2.71/2

= 6.64, 1.35

The time taken by the ball to reach the height of 150 ft are 6.64 seconds or 1.35 seconds.