SOLVING QUADRATIC EQUATION BY GRAPHING

Solve each equation by graphing.

Problem 1 :

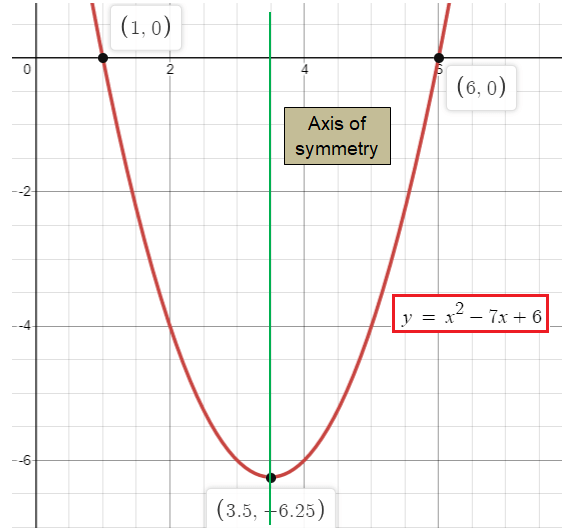
y = x² -7x + 6

Solution :

Let y = x² -7x + 6

Comparing the given equation with y = ax² + bx + c, we get

a = 1, b = -7 and c = 6

x = -b/2a

x = -(-7)/2(1)

x = 3.5

When x = 3.5

y = (3.5)² -7(3.5) + 6

y = 12.25 - 24.5 + 6

y = -6.25

The vertical line drawn at x = 3.5 will divide the parabola into two parts.

The x-intercepts should be nearer to 3.5.

When x = 1, y = 1² -7(1) + 6 ==> 0

When x = 2, y = 2² -7(2) + 6 ==> -4

When x = 5, y = 5² -7(5) + 6 ==> -4

When x = 6, y = 6² -7(6) + 6 ==> 0

Problem 2 :

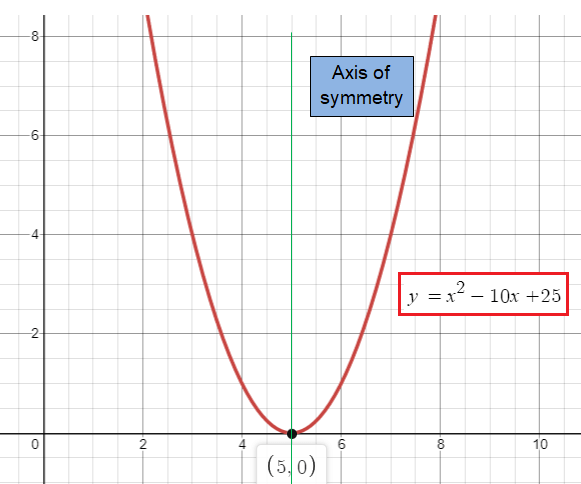
y = x² -10x + 25

Solution :

Let y = x² -10x + 25

Comparing the given equation with y = ax² + bx + c, we get

a = 1, b = -10 and c = 25

x = -b/2a

x = -(-10)/2(1)

x = 5

When x = 5

y = 5² - 10(5) + 25

y = 25 - 50 + 25

y = 0

The vertical line drawn at x = 5 will divide the parabola into two parts.

(5, 0) is a x-intercept. By tracing some more points.

When x = 3, y = 3² -10(3) + 25 ==> 4

When x = 4, y = 4² -10(4) + 25 ==> 1

When x = 6, y = 6² -10(6) + 25 ==> 1

When x = 7, y = 7² -10(7) + 25 ==> 4

Problem 3 :

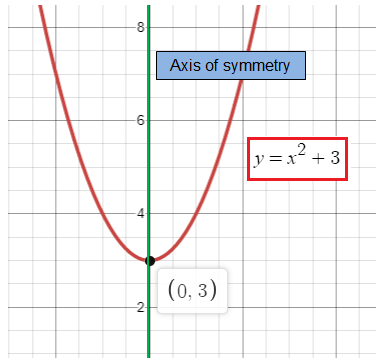
y = x² + 3

Solution :

Let y = x² + 3

Comparing the given equation with y = ax² + bx + c, we get

a = 1, b = 0 and c = 3

Axis of symmetry is at (0, 3).

So, it is not having real roots.

Problem 4 :

A football player kicks a football 2 feet above the ground with an initial vertical velocity of 75 feet per second. The function

h = −16t² + 75t + 2

represents the height h (in feet) of the football after t seconds.

(a) Find the height of the football each second after it is kicked.

(b) Use the results of part (a) to estimate when the height of the football is 50 feet.

(c) Using a graph, after how many seconds is the football 50 feet above the ground?

Solution :

h = −16t² + 75t + 2

a)

(b) From part (a), you can estimate that the height of the football is 50 feet between 0 and 1 second and between 3 and 4 seconds. Based on the function values, it is reasonable to estimate that the height of the football is 50 feet slightly less than 1 second and slightly less than 4 seconds after it is kicked.

c) To determine when the football is 50 feet above the ground, find the t-values for which h = 50.

So, solve the equation

−16t² + 75t + 2 = 50

−16t² + 75t + 2 - 50 = 0

−16t² + 75t - 48 = 0

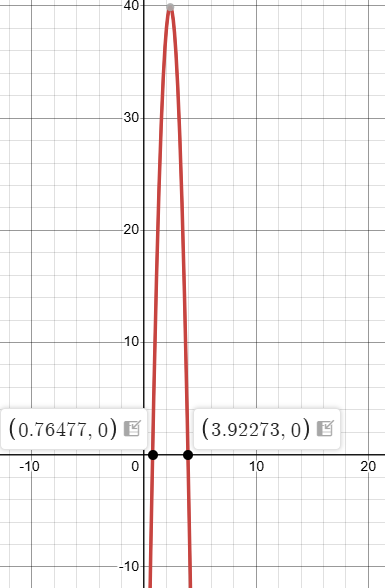
The football is 50 feet above the ground after about 0.8 second and about 3.9 seconds, which supports the estimates in part (b).

Problem 5 :

The height y (in yards) of a flop shot in golf can be modeled by y = −x² + 5x, where x is the horizontal distance (in yards).

a. Interpret the x-intercepts of the graph of the equation.

b. How far away does the golf ball land?

Solution :

y = −x² + 5x

a) Finding x-intercepts :

Put y = 0

−x² + 5x = 0

-x(x - 5) = 0

x = 0 and x = 5

So, the x-intercepts are 0 and 5.

b) The golf ball will land after 5 yards