SOLVING PROBLEMS ON ANGLE RELATIONSHIPS

Problem 1 :

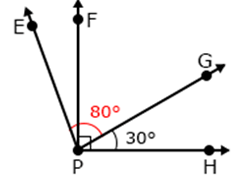
m∠EPG = 80°; m∠GPH = 30°

If ∠FPG and ∠GPH are complementary angles, then what is the measure of ∠FPG?

Solution :

m∠FPH = 90°

m∠FPG + m∠GPH = 90

m∠FPG + 30 = 90

m∠FPG = 90 - 30

m∠FPG = 60°

So, the required angle measure is 60°.

Problem 2 :

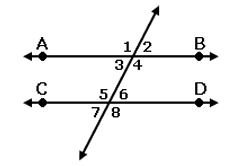
Lines AB and CD are parallel. If ∠1 measures (3x + 13)°, and ∠4 measures 151°, what is the value of x?

A. x = -4     B. x = 74     C. x = 46      D. x = 5

Solution :

∠1 = ∠4 (vertically opposite angles)

3x + 13 = 151

3x = 151 - 13

3x = 138

x = 138/3

x = 46°

So, the value of x is 46°.

Problem 3 :

Angle DOE and angle EOF are adjacent angles. If m∠DOF = 66°, m∠DOE = x, and m∠EOF = 27°, which equation could be used to solve for x?

A. x - 66° + 27° = 90°      B. x - 27° = 66°

C. x + 27° = 66°          D. x + 66° + 27° = 180°

Solution :

m∠DOF = 66°, m∠DOE = x, and m∠EOF = 27°

DOE and angle EOF are adjacent angles

m∠DOE + m∠EOF = m∠DOF

x + 27 = 66

So, option C is correct.

Problem 4 :

If ∠ROQ and ∠ROS are complementary angles, then what is the value of x and m∠ROS?

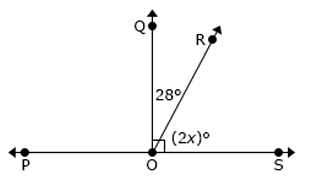
Solution :

∠QOS = ∠QOR + ∠ROS

90 = 28 + 2x

28 + 2x = 90

2x = 90 - 28

2x = 62

x = 62/2

x = 31

∠ROS = 2x

= 2(31)

 ∠ROS = 62

Problem 5 :

What is the measure of ∠GEF?

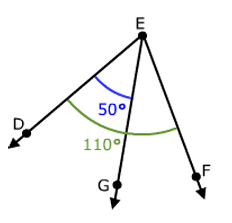
Solution :

∠DEF = 110

∠DEG + ∠GEF = 110

50 + ∠GEF = 110

∠GEF = 110 - 50

∠GEF = 60

Problem 6 :

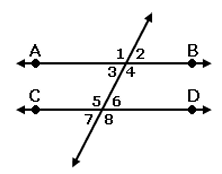
Lines AB and CD are parallel. If ∠1 measures (2x + 15)°, and ∠4 measures 111°, what is the value of x?

Solution :

∠1 = ∠4 (Vertically opposite angles)

2x + 15 = 111

2x = 111 - 15

2x = 96

x = 96/2

x = 48

Problem 7 :

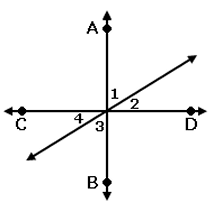
Lines AB and CD are perpendicular to each other. If ∠1 measures (4x + 3)°, and ∠2 measures 19°, what is the value of x?

Solution :

Here ∠1 and ∠2 add upto 90 degree

∠1 + ∠2 = 90

4x + 3 + 19 = 90

4x + 22 = 90

4x = 90 - 22

4x = 68

x = 68/4

x = 17

Problem 8 :

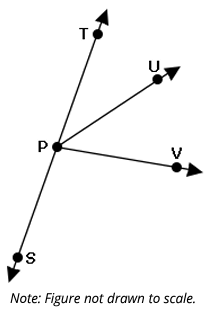
In this picture, m∠TPU = 36° and m∠UPS = 5x + 10. If ∠TPU and ∠UPS are supplementary angles, then what is the value of x?

A. 8.8      B. 134      C. 26.8      D. 30.8

Solution :

m∠TPU + m∠TPU = 180

36° + 5x + 4 = 180

5x + 40 = 180

5x = 180 - 40

5x = 140

x = 140/5

x = 28