SOLVING POLYNOMIAL EQUATIONS USING RATIONAL ROOT THEOREM

Rational Root Theorem helps us to create such a list of possible rational roots. We recall that if a polynomial has rational coefficients, then by multiplying by suitable numbers we can obtain a polynomial with integer coefficients having the same roots.

So we can use Rational Root Theorem, given below, to guess a few roots of polynomial with rational coefficient. We state the theorem without proof.

Problem 1 :

Solve the equation

x³ - 5x² - 4x + 20 = 0

Solution :

a_n = 1 and a₀ = 20

Factor of a_0, values of p = 1, 2, 4, 5, 10, 20

Factor of a_n values of q = 1

p/q = ±1, ±2, ±4, ±5, ±10, ±20

So, 2 is the solution. Then (x - 2) is the factor. By dividing the given polynomial by (x - 2) using synthetic division or long division, we can break up the given cubic polynomial into parts.

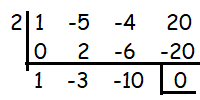
Quotient = x² - 3x - 10

Factoring this quadratic polynomial, we get

(x - 5)(x + 2)

Equating each factor to zero, that is (x - 5)(x + 2) = 0

x = 5 and x = -2

So, the three solutions of the given cubic polynomial is {-2, 2, and 5}.

List all possible rational zeroes of each function.

Problem 2 :

f(x) = 3x⁴ - 2x² + 6x - 10

Solution :

a_n = 3 and a₀ = -10

Factor of a_0, values of p = ±1, ±2, ±5, ±10

Factor of a_n values of q = ±1, ±3

So, possible rational roots are

p/q = ±1, ±2, ±5, ±10, ±1/3, ±2/3, ±5/3, ±10/3

Problem 3 :

f(x) = x³ - 10x² + 14x - 36

Solution :

a_n = 1 and a₀ = -36

Factor of a_0, values of p = ±1, ±2, ±3, ±4, ±6, ±9, ±12, ±18, ±36

Factor of a_n values of q = ±1

So, possible rational roots are,

p/q =  ±1, ±2, ±3, ±4, ±6, ±9, ±12, ±18, ±36

Problem 4 :

f(x) = x³ + 3x² - x + 8

Solution :

a_n = 1 and a₀ = 8

Factor of a_0, values of p = ±1, ±2, ±4, ±8

Factor of a_n values of q = ±1

So, possible rational roots are,

p/q = ±1, ±2, ±4, ±8

Problem 5 :

f(x) = 5 - 7x⁴ + 3x² + x -20

Solution :

f(x) = 5 - 7x⁴ + 3x² + x -20

First step should be arranging the given accordingly degree.

f(x) = - 7x⁴ + 3x² + x - 20 + 5

f(x) = - 7x⁴ + 3x² + x - 15

a_n = -7 and a₀ = -15

Factor of a_0, values of p = ±1, ±3, ±5, ±15

Factor of a_n values of q = ±1, ±7

So, possible rational roots are,

p/q = ±1, ±3, ±1/7, ±3/7, ±5/7, ±15/7

Problem 6 :

f(x) = x⁴ - 7x³ - 4x² + x - 49

Solution :

f(x) = x⁴ - 7x³ - 4x² + x - 49

a_n = 1 and a₀ = -49

Factor of a_0, values of p = ±1, ±7, ±49

Factor of a_n values of q = ±1

So, possible rational roots are,

p/q = ±1, ±7, ±49

Problem 7 :

f(x) = 2x⁴ - 5x³ + 8x² + 3x - 5

Solution :

f(x) = 2x⁴ - 5x³ + 8x² + 3x - 5

a_n = 1 and a₀ = -5

Factor of a_0, values of p = ±1, ±5

Factor of a_n values of q = ±1, ±2

So, possible rational roots are,

p/q = ±1, ±5, ±1/2, ±5/2

Problem 8 :

f(x) = 3x⁴ - 5x³ + 10x + 12

Solution :

f(x) = 3x⁴ - 5x³ + 10x + 12

a_n = 3 and a₀ = 12

Factor of a_0, values of p = ±1, ±2, ±3, ±4, ±6, ±12

Factor of a_n values of q = ±1, ±3

So, possible rational roots are,

p/q = ±1,±2, ±4, ±6, ±12, ±1/3, ±2/3, ±4/3

Problem 9 :

f(x) = 4x⁵ - 2x + 18

Solution :

f(x) = 4x⁵ - 2x + 18

a_n = 4 and a₀ = 18

Factor of a_0, values of p = ±1, ±2, ±3, ±6, ±18

Factor of a_n values of q = ±1, ±2, ±4

So, possible rational roots are,

p/q = ±1,±2, ±3, ±12, ±1/2, ±1/4, ±3/2, ±3/4, ±9/2

Problem 10 :

f(x) = 5x⁶ - 3x⁴ + 5x³ + 2x² - 15

Solution :

f(x) = 5x⁶ - 3x⁴ + 5x³ + 2x² - 15

a_n = 5 and a₀ = -15

Factor of a_0, values of p = ±1, ±3, ±5, ±15

Factor of a_n values of q = ±1, ±5

So, possible rational roots are,

p/q = ±1, ±3, ±5, ±15, ±3/5