SOLVING MULTI STEP EQUATIONS WITH FRACTIONS

Solve the following equations :

Example 1 :

20/3 = x + (19/6)

Solution :

20/3 = x + (19/6)

Subtract 19/6 on both sides.

(20/3) - (19/6) = x

Least common multiple (6, 3) is 6.

(40/6) - (19/6) = x

x = (40 - 19)/6

x = 21/6

x = 7/2

Example 2 :

-61/12 = x - (4/3)

Solution :

-61/12 = x - (4/3)

Add 4/3 on both sides.

(-61/12) + (4/3) = x

Least common multiple (12, 3) is 12.

(-61/12) + (16/12) = x

x = (-61 + 16) / 12

x = -45/12

x = -15/4

Example 3 :

7/12 = (7/9) x

Solution :

7/12 = (7/9) x

Multiply by 9/7 on both sides.

(7/12) ⋅ 9/7 = x

x = 9/12

x = 3/4

Example 4 :

(-22/9)x = 11/9

Solution :

(-22/9)x = 11/9

Multiply by -9/22 on both sides.

x = (11/9) ⋅ (-9/22)

x = -1/2

Example 5 : 

9/4 = (-3/2) x + 4  3/4

Solution :

9/4 = (-3/2) x + 4  3/4

Converting the mixed fraction as improper fraction, we get

9/4 = (-3/2) x + 19/4

Subtracting 19/4 on both sides.

9/4 - 19/4 = -3x/2

(9 - 19)/4 = -3x/2

-10/4 = -3x/2

-5/2 = -3x/2

Multiply by 2 on both sides.

-5 = -3x

Divide by -3 on both sides.

x = 5/3

Example 6 :

-11/2 = -2  1/3 + (3  1/6) x

Solution :

-11/2 = -2  1/3 + (3  1/6) x

Converting the mixed fraction to improper fraction, we get

-11/2 = (-7/3) + 19x/6

Add 7/3 on both sides.

-11/2 + 7/3 = 19x/6

Least common multiple (2, 3) is 6

(-33 + 14)/6 = 19x/6

-19/6 = 19x/6

Multiply by 6 on both sides.

-19 = 19x

Divide by 19 on both sides.

x = -1

Example 7 :

(5/7) (3/2 + x) = 145/84

Solution :

(5/7) (3/2 + x) = 145/84

Multiply by 5/7 on both sides.

(3/2 + x) = (145/84) ⋅ (7/5)

3/2 + x = 29/12

Subtracting 3/2 on both sides.

x = 29/12 - 3/2

Least common multiply (12, 2) is 12

x = (29 - 18)/12

x = 11/12

Example 8 :

(7/4)(x - 1) = 7/8

Solution :

(7/4)(x - 1) = 7/8

Multiply by 4/7 on both sides.

x - 1 = (7/8) ⋅ (4/7)

x - 1 = 1/2

Add 1 on both sides.

x = 1/2 + 1

x = 3/2

Example 9 :

Use the table to find the number of miles x you need to bike on Friday so that the mean number of miles biked per day is 5.

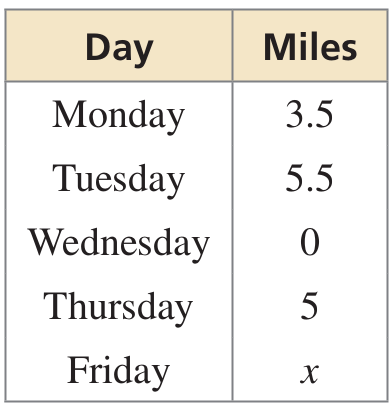
Solution :

Mean number of miles = 5

(3.5 + 5.5 + 0 + 5 + x)/5 = 5

(14 + x)/5 = 5

14 + x = 25

x = 25 - 14

x = 11

So, the number of miles to be covered on Friday is 11.

Example 10 :

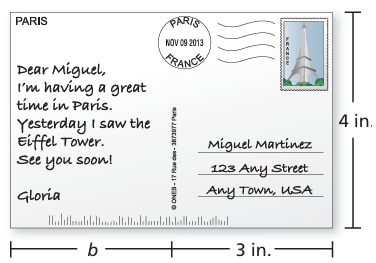
The area of the postcard is 24 square inches. What is the width b of the message (in inches)?

Solution :

Area of rectangular postcard = length x width

Length = (b + 3) inches

Width =4 inches

Area = (b + 3) 4

24 = 4(b + 3)

b + 3 = 24/4

b + 3 = 6

b = 6 - 3

b = 3 inches

So, the value of b is 3 inches.

Example 11 :

You order two servings of pancakes and a fruit cup. The cost of the fruit cup is $1.50. You leave a 15% tip. Your total bill is $11.50. How much does one serving of pancakes cost?

Solution :

Cost of fruit cup = $1.50

Tip = 15%

Total bill = $11.50

Let x be the cost of one serving.

115% of (2x + 1.5) = 11.50

1.15(2x + 1.5) = 11.50

2x + 1.5 = 11.50/1.15

2x + 1.5 = 10

2x = 10 - 1.5

2x = 8.5

x = 8.5/2

x = 4.25

Cost of one serving is $4.25

Example 12 :

The circles are identical. What is the area of each circle?

a) 2    b)  4     c)  16π     d)  64π

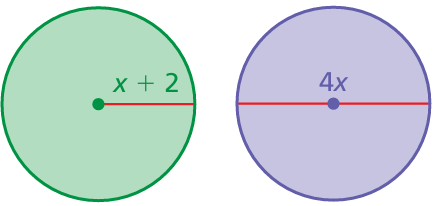
Solution :

Radius of first circle = x + 2

Radius of second circle = 4x/2

= 2x

2x = x + 2

2x - x = 2

x = 2

Radius = 2 + 2 ==> 4

Area of circle = πr²

= π(4²)

= 16 π

Example 13 :

A boat travels x miles per hour upstream on the Mississippi River. On the return trip, the boat travels 2 miles per hour faster. How far does the boat travel upstream?

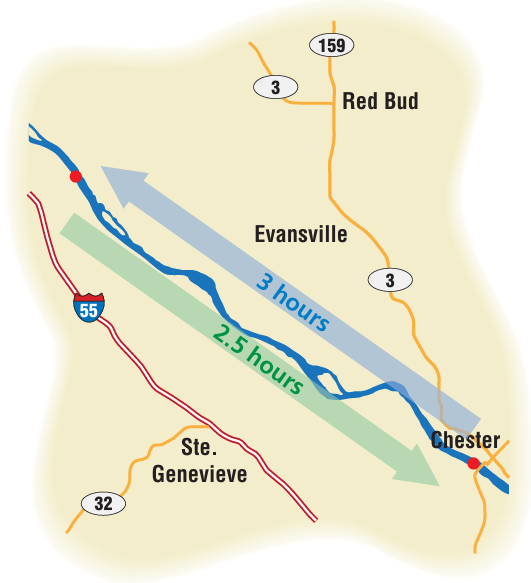
Solution :

The speed of the boat on the return trip is (x + 2) miles per hour.

Distance upstream = Distance of return trip

3x = 2.5(x + 2)

3x = 2.5x + 5

3x - 2.5x = 5

0.5x = 5

x = 5/0.5

x = 10

Speed of the trip is 10 + 2 ==> 12 miles per hour