SOLVING LOGARITHMIC INEQUALITIES WITH DIFFERENT BASES
To solve logarithmic inequalities with different bases, we have to follow the procedure given below.
Step 1 :
Using the properties of logarithm, we have to simplify and solve for the variable.
Using change of base rule, we can interchange the base and argument.
Step 2 :
Find the domain for each logarithmic expressions and write the solution in the number line.
Step 3 :
The intersection domain and the values of x solved using the procedure given above is the solution.
Solve the following logarithmic inequalities.
Problem 1 :
Solution :
|
x + 1 > 0 x > -1 |
2 - x > 0 -x > -2 x < 2 |
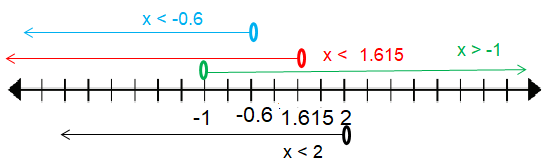
The intersection part is,
Problem 2 :
Solution :
(-∞, -1.5) (-1.5, -1) and (-1, ∞)
Choosing values from each interval,
2x2 + 5x + 3 ⩾ 0
(-∞, -1.5)
When x = -5
2(25)+5(-5)+3
50-25+3 ⩾ 0
Satisfies
2x2 + 5x + 3 ⩾ 0
(-1.5, -1)
When x = -1.25
2(1.5625)+5(-1.25)+3
3.125 - 6.25 + 3
= -0.125
Does not satisfy
2x2 + 5x + 3 ⩾ 0
(-1, ∞)
When x = 0
2(0)+5(0)+3
= 3
Satisfies
|
2x2 + 3x + 1 > 0 (2x + 1)(x + 1) > 0 x > -1/2 and x > -1 |
2x + 2 > 0 2x > -2 x > -1 |
The intersection of all solution is (-0.5, ∞).
Problem 3 :
Solution :
Decomposing into intervals,
(-∞, 7) and (7, ∞)
x + 2 < 9
When x = 0 ∈ (-∞, 7)
0 + 2 < 9
2 < 9 true
x + 2 < 9
When x = 8 ∈ (7, ∞)
8 + 2 < 9
10 < 9 false
Domain of given logarithmic expressions :
|
x2 - x - 6 > 0 (x - 3)(x + 2) > 0 x > 3 and x > -2 |
x - 3 > 0 x > 3 |
Intersection part is (3, 7). So, the solution is (3, 7).
Problem 4 :
Solution :
Decomposing into intervals, we get
(-∞, 3/14)(3/14, 1) and (1, ∞)
When x = -1 ∈ (-∞, 3/14)
(x - 1)(14x - 3) ⩾ 0
(-1 - 1)(-14 - 3) ⩾ 0
17 ⩾ 0
True
When x = 0.5 ∈ (3/14, 1)
(x - 1)(14x - 3) ⩾ 0
(0.5 - 1)(7 - 3) ⩾ 0
-0.5(2) ⩾ 0
-1 ⩾ 0
False
When x = 2 ∈ (1, ∞)
(x - 1)(14x - 3) ⩾ 0
(2 - 1)(28 - 3) ⩾ 0
1(25) ⩾ 0
25 ⩾ 0
True
|
2x2 + x + 1 > 0 (2x + 1) (x + 1) > 0 x > -1/2 and x > -1 |
2x - 1 > 0 x > 1/2 |
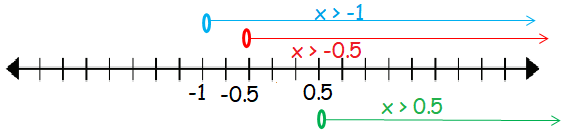
Considering (-∞, 3/14) (1, ∞) and the above shaded region, we get
(1, ∞) is the solution
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling