SOLVING LOGARITHMIC EQUATIONS USING PROPERTIES

To solve a logarithmic equation, first combine the logarithmic terms using rules of logarithms.

Some of the rules in logarithm :

log m + log n = log (m x n)

log m - log n = log (m / n)

log mⁿ = n log m

log _a a = 1

After combining more than one logarithmic terms as one term, we have to convert logarithmic form to exponential form then solve for the variable.

Conversion from logarithmic form to exponential form :

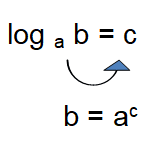
Solve the following logarithmic equations :

Problem 1 :

log₇ 3 + log₇ x = log₇ 32

Solution :

log₇ 3 + log₇ x = log₇ 32

log_a m + log_a n = log_a mn

log₇ (3x) = log₇ 32

3x = 32

x = 32/3

Problem 2 :

2 log₆ 4x = 0

Solution :

2 log₆ 4x = 0

log₆ 4x = 0

4x = 6⁰

4x = 1

x = 1/4

Problem 3 :

log₂ x + log₂ (x - 3) = 2

Solution :

log₂ x + log₂ (x - 3) = 2

log₂ (x) (x - 3) = 2

log₂ (x² - 3x) = 2

x² - 3x = 2²

x² - 3x = 4

x² - 3x - 4 = 0

x² - 4x + x - 4 = 0

x(x - 4) + 1 (x - 4) = 0

(x - 4) (x + 1) = 0

x = 4 or x = -1

Problem 4 :

log₂ (x + 5) - log₂ (x - 2) = 3

Solution :

log₂ (x + 5) - log₂ (x - 2) = 3

log₂ (x + 5 / x - 2) = 3

log₂ (x + 5 / x - 2) = log₂ 2³

(x + 5) / (x - 2) = 8

x + 5 = 8(x - 2)

x + 5 = 8x - 16

8x - x = 16 + 5

7x = 21

x = 3

Problem 5 :

4 ln (2x + 3) = 11

Solution :

4 ln (2x + 3) = 11

ln (2x + 3) = 11/4

ln (2x + 3) = 2.75

2x + 3 = e^2.75

2x + 3 = 15.6426

2x = 15.6426 - 3

2x = 12.6426

x = 12.6426/2

x = 6.321

Problem 6 :

log x - log 6 = 2 log 4

Solution :

log x - log 6 = 2 log 4

log (x/6) = log 4²

x/6 = 4²

x/6 = 16

x = 16 × 6

x = 96

Problem 7 :

log 2x = 1.5

Solution :

log 2x = 1.5

2x = 10^1.5

x = 10^1.5/2

x = 31.62/2

x = 15.81

Problem 8 :

log₂ 2x = -0.65

Solution :

log₂ 2x = -0.65

2x = 2^-0.65

2x = 0.637

x = 0.637/2

x = 0.32

Problem 9 :

1/3 log₂ x + 5 = 7

Solution :

1/3 log₂ x + 5 = 7

1/3 log₂ x = 7 - 5

1/3 log₂ x = 2

log₂ x = 6

x = 2⁶

Problem 10 :

4 log₅ (x + 1) = 4.8

Solution :

4 log₅ (x + 1) = 4.8

log₅ (x + 1) = 4.8/4

log₅ (x + 1) = 1.2

x + 1 = 5^1.2

x = 5^1.2 - 1

x = 6.90 - 1

x = 5.90

Problem 11 :

log₂ x + log₂ 3 = 3

Solution :

log₂ x + log₂ 3 = 3

log₂ (3x) = 3

3x = 2³

3x = 8

x = 8/3

Problem 12 :

2 log₄ x - log₄ (x - 1) = 1

Solution :

2 log₄ x - log₄ (x - 1) = 1

log₄ x² - log₄ (x - 1) = 1

log₄ (x²/x - 1) = 1

x²/x - 1 = 4

x² = 4(x - 1)

x² = 4x - 4

x² - 4x + 4 = 0

(x - 2) (x - 2) = 0

x = 2

Solve the equation. Check for extraneous solutions.

Problem 13 :

ln (7x − 4) = ln (2x + 11)

Solution :

ln (7x − 4) = ln (2x + 11)

7x - 4 = 2x + 11

7x - 2x = 11 + 4

5x = 15

x = 15/5

x = 3

Problem 14 :

log₂(x − 6) = 5

Solution :

log₂(x − 6) = 5

x - 6 = 2⁵

x - 6 = 32

x = 32 + 6

x = 38

Problem 15 :

log 5x + log (x − 1) = 2

Solution :

log 5x + log (x − 1) = 2

log [5x(x - 1)] = 2

5x(x - 1) = 10²

5x² - 5x = 100

5x² - 5x - 100 = 0

x² - x - 20 = 0

x² - 5x + 4x - 20 = 0

x(x - 5) + 4(x - 5) = 0

(x + 4)(x - 5) = 0

x = -4 and x = 5

Problem 16 :

log₄(x + 12) + log₄ x = 3

Solution :

log₄(x + 12) + log₄ x = 3

log₄ [(x + 12)x] = 3

[x(x + 12)] = 4³

x² + 12x = 64

x² + 12x - 64 = 0

x² + 16x - 4x - 64 = 0

x(x + 16) - 4(x + 16) = 0

(x - 4)(x + 16) = 0

x = 4 and x = -16