SOLVING LINEAR FUNCTION WORD PROBLEMS

Problem 1 :

Mrs. Morris gave her students this pattern of white tiles.

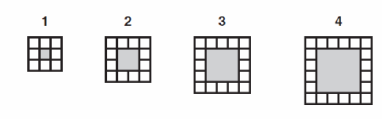
She asked her students to write an equation to represent the number of white tiles t for any figure number n,

which equation represents the number of white tiles in the pattern.

a) t = n + 2      b)  t = n + 4      c)  t = 4n + 4    d)  t = 4n + 8

Solution :

Observing the number of white tiles, it increases 4 every time. So, the answer is c.

Problem 2 :

The chart shows the amount of total salary (commission plus base salary) paid to employees of a store that specializes in big screen televisions.

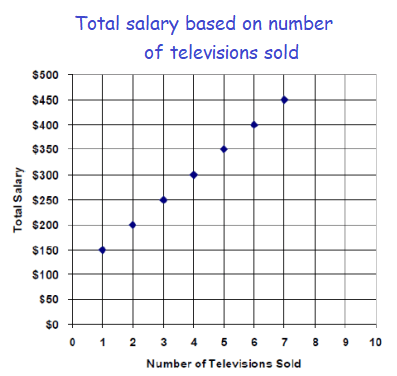
Which equation best represents the total salary (T) that an employee makes for selling any number of television sets (n) ?

a)  T = 50n + 100     b)  100(n + 50)

c) T = 100n + 50      d)  T = 50(n + 100)

Solution :

Taking two points from the scatter plot, we get

(1, 150) and (2, 200)

m = (200 - 150)/(2 - 1)

= 50/1

m = 50

y = 50x + b

Tracing one of the points from scatter plot (3, 250)

250 = 50(3) + b

250 - 150 = b

b = 100

Problem 3 :

A school purchases boxes of candy bars. 

• Each box contains 50 candy bars.
• Each box cost $30

How much does the school have to charge for each candy bar to make a profit of $10 per box ?

a)  $0.40    b)  $0.50    c)  $0.80    b)  $1.25

Solution :

Cost of 1 box = $30

Profit = $10

Cost of each box with profit of $10 = 40

Cost of each candy = 40/50

= 0.80

Cost of each candy is $0.80.

Problem 4 :

Which equation is equivalent to y + 2(x + 5) = 4x + 5

a)  y = 2x + 20    b)  y = -4x + 5

c)  y = 2x - 5    b)  y = 5x + 2

Solution :

y + 2(x + 5) = 4x + 5

y + 2x + 10 = 4x + 5

y = 4x - 2x + 5 - 10

y = 2x - 5

So, y = 2x - 5 is the correct.

Problem 5 :

Jessie's bus ride to school is 5 minutes more than 2/3 the time Robert's bus ride. Which graph shows the possible times of Jessie's and Robert's bus rides ?

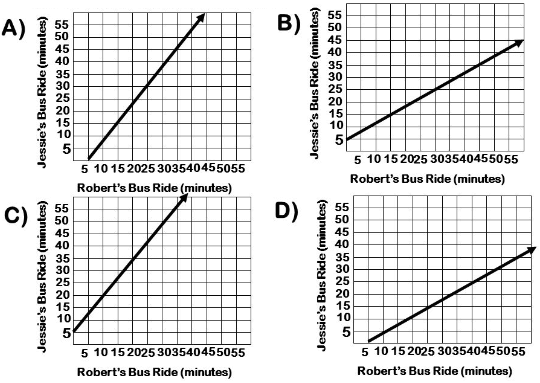
Solution :

Option A :

Taking two points from the graph, 

(5, 0) and (25, 30)

Slope (m) = (30 - 0) / (25 - 5)

= 30/20

= 3/2

So, option A is not correct.

Option B : 

Taking two points from the graph, 

(0, 5) and (15, 15)

Slope (m) = (15 - 5) / (15 - 0)

= 10/15

= 2/3

So, option B is correct.

Problem 6 :

Dennis is compared the y-intercept of the graph of the function f(x) = 3x + 5 to the y-intercept of the graph of the linear function that includes the points in the table below.

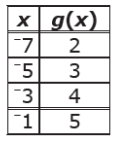
What is the difference when the y-intercept of f(x) is subtracted from y-intercept of g(x) 

a)  -11      b)  -9.3     c)  0.5     d) 5.5

Solution :

f(x) = 3x + 55

y-intercept of f(x) is 5.

From the given table, we find the y-intercept since it is not given.

(-7, 2) and (-5, 3)

Slope (m) = (3 - 2) / (-5 + 7)

m = 1/2

y = (1/2)x + b

The line g(x) is passing through the point (-1, 5)

5 = (1/2) (-1) + b

b = 5 + 1/2

b = 11/2 ==> 5.5

y-intercept of g(x) = 5.5

Difference between g(x) and f(x) = 5.5 - 5

= 0.5

Problem 7 :

The boiling point of water, T (measured in degrees), at altitude a (measured in feet) is modeled by the function

T(a) = -0.0018a + 212

In terms of altitude and temperature, which statement describes the meaning of slope ?

a)  The boiling point increases by 18 degrees as the altitude increases 1000 feet.

b)  The boiling point increases by 1.8 degrees as the altitude increases 1000 feet.

c)  The boiling point decreases by 18 degrees as the altitude increases 1000 feet.

d)  The boiling point decreases by 1.8 degrees as the altitude increases 1000 feet.

Solution :

Slope is negative,

Slope = -0.0018

Converting into fraction, we get

= -18/10000

= -1.8/1000

So, option d is correct.

Problem 8 :

Mario compared the slope of the function graphed below to the slope of the linear function that has an x-intercept of 4/3 and a y-intercept of -2.

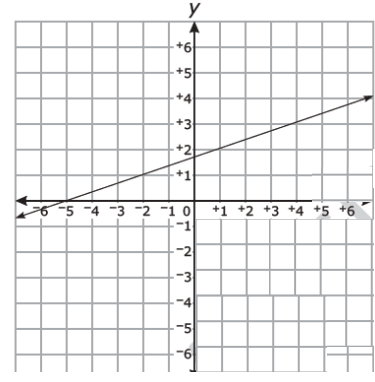
What is the slope of the function with smaller slope ?

a)  1/5    b)   1/3    c)  3   d) 5

Solution :

x-intercept = 4/3,  y-intercept = -2

Equation of the line :

Slope of the line given :

Taking two points from the graph, (-2, 1) and (1, 2)

Slope = (2 - 1) / (1 + 2)

m = 1/3

3/2 > 1/3

Smaller slope = 1/3

Problem 9 :

The table shows the distance a car has traveled

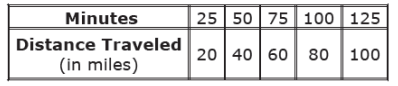
What is the meaning of slope of the liner model for the data ?

a) The car travels 5 miles every minute

b) The car travels 4 miles every minute

c) The car travels 4 miles every 5 minutes

d)  The car travels 5 miles every 4 minutes

Solution :

Taking two points from the table

(25, 20) (50, 40)

m = (40 - 20) / (50 - 25)

m = 20/25

m = 4/5

The car travels 4 miles for every 5 minutes

Problem 10 :

Cell phone company Y charges a $10 start up fee plus $0.10 per minute x, Cell phone company Z charges $0.20 per minute, x with no start up fee. Which function represents the difference in cost between Company Y and Company Z 

a) f(x) = -0.10x - 10      b)  f(x) = -0.10x + 10

c) f(x) = 10x - 0.10      d)  f(x) = 10x + 0.10

Solution :

Charges of Company Y :

f(x) = 10 + 0.10x ---(1)

Charges of Company Z :

f(x) = 0.20x ---(2)

(1) - (2)

f(x) = (10 + 0.10x) - 0.20x

= 10 + 0.10x - 0.20x

f(x) = 10 - 0.10x

So, option b is correct.

Problem 11 :

What is the value of w in the equation

Solution :

Problem 12 :

What is the slope of the line containing the points (-9, 2) and (3, 14)?

Solution :

Slope m = (y₂ - y₁)/(x₂ - x₁)

m = (14 - 2) / (3 + 9)

m = 12/12

m = 1