SOLVING INEQULAITIES INVOLVING QUADRATIC FUNCTIONS

To solve quadratic inequalities in the form of

ax² + b ≥ c or ax² + b ≤  c

ax² + b > c or ax² + b <  c

we follow the steps given below.

• Change the inequality signs as equal sign and find critical points.
• We will get two different values for x.
• Plot it on the number line.
• Decompose into intervals.
• Choosing one of the points from the interval and applying the inequality given, if the given inequality satisfies by the values we can say those intervals are solutions.

Find the solutions of the following inequalities :

Problem 1 :

x² + 6 ≥ 22

Solution :

To find critical points, change the ≥ as =.

x² + 6 = 22

Subtracting 6 on both sides.

x² = 22 – 6

x² = 16

x = ±4

After plotting these values in the number line, we get the intervals

(-∞, -4], [-4, 4] and [4, ∞)

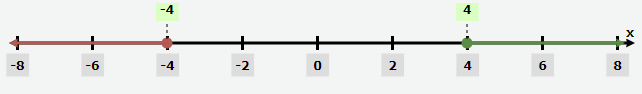
• (-∞, -4] satisfies the original inequality given.
• [-4, 4] doesn't satisfy the original inequality.
• [4, ∞) satisfies the original inequality given.

So, the solution is (-∞, -4] and [4, ∞).

Find the solutions of the following inequalities :

Problem 2 :

3x² - 4 ≥ 8

Solution :

To find critical points, change the ≥ as =.

3x² - 4 ≥ 8

Finding critical points :

3x² = 8 + 4

3x² = 12

Dividing 3 on both sides.

3x²/3 = 12/3

x² = 4

x = √4

x = ±2

Critical points are -2 and 2.

So, the solution is (-∞, -2] and [2, ∞).

Problem 3 :

5x² - 20 < 105

Solution :

To find critical points, change the < as =.

5x² - 20 = 105

Finding critical points :

5x² = 105 + 20

5x² = 125

Dividing 5 on both sides.

5x²/5 = 125/5

x² = 25

x = √25

x = ±5

Critical points are -5 and 5.

So, the solution is (-5, 5).

Problem 4 :

4x² < 1

Solution :

To find critical points, change the < as =.

4x² = 1

Dividing 4 on both sides.

4x²/4 = 1/4

x² = 1/4

x = √(1/4)

x = ±1/2

Plotting the critical points on the number line and use the testing points, we get

So, the solution is (-1/2, 1/2).

Problem 5 :

9x² ≥ 4

Solution :

To find critical points, change the ≥ as =.

9x² = 4

Dividing 9 on both sides.

9x²/9 = 4/9

x² = 4/9

x = √(4/9)

x = ±2/3

So, the critical points are -2/3 and 2/3.

Plotting the critical points on the number line and use the testing points, we get

So, the solution is (-∞, -2/3] and [2/3, ∞).

Problem 6 :

25x² - 2 ≥ 2

Solution :

To find critical points, change the ≥ as =.

25x² - 2 = 2

25x² = 2 + 2

25x² = 4

Dividing 25 on both sides.

25x²/25 = 4/25

x² = 4/25

x = √(4/25)

x = ±2/5

So, the critical points are -2/3 and 2/3.

So, the solution is (-∞, -2/5] and [2/5, ∞).

Problem 7 :

36x² + 7 ≤ 11

Solution :

To find critical points, change the ≤ as =.

36x² + 7 = 11

36x² = 11 – 7

36x² = 4

Dividing 36 on both sides.

36x²/36 = 4/36

x² = 4/36

x² = 1/9

x = √(1/9)

x = ±1/3

So, the critical points are -1/3 and 1/3.

So, the solution is [-1/3, 1/3].

Problem 8 :

2(x² – 5) < 8

Solution :

Toa find critical points, change < as =.

2(x² – 5) = 8

2x² – 10 = 8

2x² = 8 + 10

2x² = 18

Dividing 2 on both sides.

2x²/2 = 18/2

x² = 9

x = √9

x = ±3

So, the critical points are -3 and 3.

So, the solution is (-3, 3).

Problem 9 :

(x² + 6)/2 ≥ 53

Solution :

To find critical point, change ≥ as =.

(x² + 6)/2 = 53

Multiplying 2 on both sides.

x² + 6 = 106

x² = 106 – 6

x² = 100

x = √10

x  = ±10

So, the critical points are -10 and 10.

So, the solution is (-10, 10).

Problem 10 :

10 - x² > 6

Solution :

To find critical point, change ≥ as =.

10 - x² = 6

- x² = 6 – 10

-x² = -4

x² = 4

x = ±2

So, the critical points are -2 and 2.

So, the solution is (-2, 2).

Problem 11 :

15 - 2x² ≤ -3

Solution :

To find critical point, change ≥ as =.

15 - 2x² = -3

- 2x² = -3 – 15

-2x² = -18

Dividing -2 on both sides.

-2x²/-2 = -18/-2

x² = 9

x = √9

x = ±3

The critical points are -3 and 3.

So, the solution is (-∞, -3) and (3, ∞).

Problem 12 :

10 ≤ 12 – 8x²

Solution :

10 = 12 – 8x²

10 – 12 = – 8x²

-2 = -8x²

Dividing -2 on both sides.

-2/-2 = -8x²/-2

1 = 4x²

Dividing 4 on both sides.

1/4 = 4/4x²

1/4 = x²

√(1/4) = x

±1/2 = x

Critical points are -1/2 and 1/2.

So, the solution is (-1/2, 1/2).