SOLVING INEQUALITIES BY MULTIPLYING OR DIVIDING

Use a table to solve the inequality.

Problem 1 :

4x < 4

Solution :

4x < 4

Divide it by 4 both sides.

4x/4 < 4/4

x < 1

Problem 2 :

-2x ≤ 2

Solution :

-2x ≤ 2

Divide by -2 on both sides.

x ≥ 2/(-2)

x ≥ -1

Problem 3 :

-5x > 15

Solution :

-5x > 15

Divide it by -5 on both sides.

x < 15/(-5)

x < -3

Problem 4 :

x/-3 ≥ 1

Solution :

x/-3 ≥ 1

Divide it by -3 on both sides.

x ≤ 1/(-3)

x ≤ -3

Problem 5 :

x/-2 > 5/2

Solution :

x/-2 > 5/2

Multiply by -2 on both sides.

x < -5

Problem 6 :

x/4 ≤ 3/8

Solution :

x/4 ≤ 3/8

Multiply by 4 on both sides, we get

x ≤ (3/8)⋅4

x ≤ (3/2)

Solve the inequality. Graph the solution.

Problem 1 :

3n > 18

Solution :

3n > 18

Divide each side by 3.

3n/3 > 18/3

n > 6

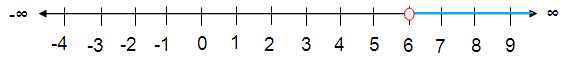
Problem 2 :

c/4 ≤ -9

Solution :

c/4 ≤ -9

Multiply each side by 4.

(c/4) × 4 ≤ -9 × 4

c ≤ -36

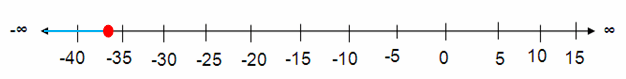
Problem 3 :

1.2m < 12

Solution :

 

1.2m < 12

Divide each side by 1.2.

(1.2/1.2)m < 12/1.2

m < 10

Problem 4 :

-14 > x ÷ 2

Solution :

-14 > x ÷ 2

Multiply each side by 2.

-14 × 2 > (x/2) × 2

-28 > x

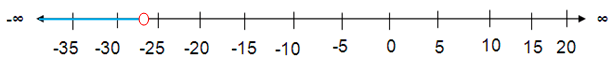
Problem 5 :

w/5 ≥ -2.6

Solution :

w/5 ≥ -2.6

Multiply each side by 5.

(w/5) × 5 ≥ -2.6 × 5

w ≥ -13

Problem 6 :

5 < 2.5k

Solution :

Given, 5 < 2.5k

Divide each side by 2.5.

5/2.5 < 2.5/2.5k

2 < k

k > 2

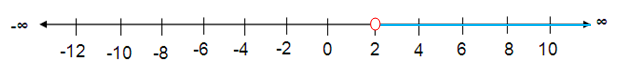
Problem 7 :

4x ≤ -3/2

Solution :

Given, 4x ≤ -3/2

Multiply each side by 2.

(4x) × 2 ≤ (-3/2) × 2

8x ≤ -3

Divide each side by 8.

(8x)/8 ≤ -3/8

x ≤ -3/8

Problem 8 :

2.6y ≤ -10.4

Solution :

Given, 2.6y ≤ -10.4

Divide each side by 2.6.

2.6/2.6y ≤ -10.4/2.6

y ≤ -4

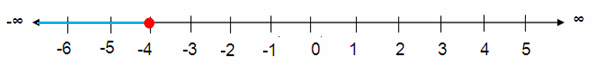
Problem 9 :

10.2 > b/3.4

Solution :

Given,10.2 > b/3.4

Multiply each side by 3.4.

10.2 × 3.4 > (b/3.4) × 3.4

34.68 > b

b < 34.68

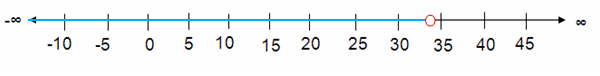
Problem 10 :

The tallest person who ever lived was approximately 8 feet 11 inches tall.

a. Write an inequality that represents the heights of every other person who has ever lived.

b. Is 9 feet a solution of the inequality? Explain.

Solution :

a) 1 feet = 12 inches

8 feet = 8 x 12

= 96 inches

= 96 + 11

= 107 inches

Let h be the height.

h < 107

b) 9 feet = 9 x 12

= 108

9 feet is not the solution.

Problem 11 :

The winner of a weight-lifting competition bench-pressed 400 pounds. The other competitors all bench-pressed at least 23 pounds less.

a. Write an inequality that represents the weights that the other competitors bench-pressed.

b. Was one of the other competitors able to bench-press 379 pounds? Explain.

Solution :

To find the maximum weight an opponent could have lifted, subtract the minimum difference from the winner's total. The winner lifted 400 pounds, and the others lifted at least 23 pounds less:

400 - 23 ==> 377

This means the highest possible weight any other competitor lifted was 377 pounds. 

Let x represent the weight bench-pressed by any other competitor. Since their weight must be 377 pounds or lower, the inequality is:

x ≤ 377

b) 379 ≤ 377

This statement is false because 379 is greater than 377. Therefore, 379 pounds does not satisfy the condition of being "at least 23 pounds less" than the winner's score.

Problem 12 :

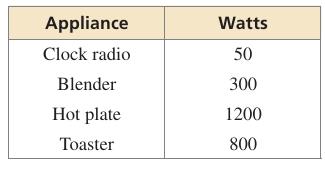
A circuit overloads at 1800 watts of electricity. You plug a microwave oven that uses 1100 watts of electricity into the circuit.

a. Write and solve an inequality that represents how many watts you can add to the circuit without overloading the circuit.

b. In addition to the microwave oven, which of the following appliances can you plug into the circuit at the same time without overloading the circuit

Solution :

Watts used by microwave oven + Additional watts < Overload wattage

Let w be the additional watts you can add to the circuit. 

1100 + w < 1800

Subtracting 1100 on both sides, we get

w < 700

You can add up to 700 watts to the circuit, which means that you can also plug in the clock radio and the blender.

You can check that your answer is correct by adding the numbers of watts used by the microwave oven, clock radio, and blender.

1100 + 50 + 300 = 1450

The circuit will not overload because the total wattage is less than 1800 watts.