SOLVING EQUATIONS WITH nth ROOTS

Find the real solution(s) of the following.

Problem 1 :

4x⁵ = 128

Solution :

4x⁵ = 128

Divide by 4 on both sides.

x⁵ = 128/4

x⁵ = 32

Taking 5th root on both sides, we get

5^th root (x) = 5^th root (32)

5^th root (x) = 5^th root (2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2)

= 2

So, the value of x is 2.

Problem 2 :

(x − 3)⁴ = 21

Solution :

(x − 3)⁴ = 21

Take 4^th root on both sides, we get

x - 3 =  ∜21

x - 3 = ±2.14

x - 3 = 2.14 and x - 3 = -2.14

x = 2.14 + 3 and x = -2.14 + 3

x = 5.14 and x = 0.86

Find the real solution(s) of the equation. Round your answer to two decimal places when appropriate.

Problem 3 :

8x³ = 64

Solution :

8x³ = 64

Dividing by 8 on both sides, we get

x³ = 64/8

x³ = 8

Taking cube roots on both sides, we get 

x =  ∛8

= ∛(2 ⋅ 2 ⋅ 2)

x = 2

Problem 4 :

(1/2) x⁵ = 512

Solution :

(1/2) x⁵ = 512

Multiplying by 2 on both sides, we get

x⁵ = 512(2)

x⁵ = 1024

Taking 5th root on both sides.

x = 5^th root (1024)

x = 5^th root (4 ⋅ 4 ⋅ 4 ⋅ 4 ⋅ 4)

x = 4

Problem 5 :

(x + 5)⁴ = 16

Solution :

(x + 5)⁴ = 16

Taking 4^th root on both sides, we get

(x + 5) = ∜16

(x + 5) = ∜(2 ⋅ 2 ⋅ 2 ⋅ 2)

x + 5 = ±2

x + 5 = 2 and x + 5 = -2

x = 2 - 5 and x = -2 - 5

x = -3 and x = -7

Problem 6 :

(x − 2)³ = −14

Solution :

(x − 2)³ = −14

Take cube root on both sides.

x - 2 = ∛-14

x - 2 = -2.41

Add 2 on both sides.

x = -2.41 + 2

x = -0.41

Find the radius of the figure with the given volume.

Problem 7 :

V = 216 ft³

Solution :

Volume of sphere = (4/3)πr³

(4/3)πr³ = 216

r³ = 216 (3/4) (1/π)

r³ = 51.59

r = 3.7 ft

Problem 8 :

Volume 1332 ft³

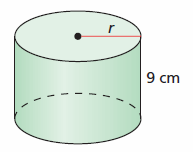
Solution :

Volume of sphere = πr² h

πr² h = 1332

πr² 9 = 1332

r² = (1332/9)(1/π)

r² = (1332/9)(1/π)

r = 6.86 cm

Problem 9 :

Out of a group of 50,000 births, the number of people, f(x) surviving to age x is modeled by the function f (x) = 5000√(100−x).

a. How many people in the group are expected to survive to age 80?

b. At what age are 35,000 people in the group still surviving?

Solution :

f(x) = 5000√(100−x)

a)  When x = 80

f (80) = 5000√(100 − 80)

= 5000√20

= 5000 (4.47)

= 22360.67

About 22,360 people are expected to survive to age 80.

b) Wehn f(x) = 35000

35000 = 5000√(100−x)

√(100−x) = 35000/5000

√(100−x) = 7

100 - x = 7²

-x = 49 - 100

-x = -51

x = 51

Problem 10 :

Between which two consecutive integers does ⁴√125 lie? Explain your reasoning.

Solution :

⁴√125 = ⁴√(5 x 5 x 5)

= 3.34

⁴√125 is lie between 3 and 4.

Problem 11 :

Describe and correct the error in evaluating the expression.

Solution :

= 27^2/3

Writing 27 in expanded form, we get

= (3³)^2/3

= 3^{3 x (2/3)}

= 3²

= 9

The error is after cancelling 3, we get 3². Which is 9.

Problem 12 :

Solution :

= 256^4/3

Writing 256 in expanded form, we get

256 = 4 x 4 x 4 x 4

= (4⁴)^4/3

= 4^{4 x (4/3)}

= 4^16/3

Since we write 4/3 as 4 x 1/3, there should be cube root. But it is written as 4^16/3

Problem 13 :

Match the equivalent expressions. Explain your reasoning.

Solution :

1)  (³√5)⁴

= (5^1/3)⁴

= 5^{(1/3) x 4}

= 5^(4/3)

2)  (⁴√5)³

= (5^(1/4))³

= 5^{(1/4) x 3}

= 5^(3/4)

3)  1/⁴√5

= 1/5^1/4

Bringing the denominator to numerator, we change the sign of the exponent.

= 5^-1/4

4)  -⁴√5

= -5^1/4

Find the real solution(s) of the equation. Round your answer to two decimal places when appropriate.

1) --> b), 2) --> d), 3 --> a), 4) --> c

Problem 14 :

x³ = 125

Solution :

x³ = 125

Writing 125 in expanded form, we get

125 = 5 x 5 x 5

x³ = 5³ 

Since the powers are equal, we can equate the bases.

x = 5

So, the valeu of x is 5.

Problem 15 :

5x³ = 1080

Solution :

5x³ = 1080

x³ = 1080/5

x³ = 216

216 = 6 x 6 x 6

x³ = 6³

x = 6

Problem 16 :

(x + 10)⁵ = 70

Solution :

(x + 10)⁵ = 70

(x + 10) = 70^1/5

x + 10 = 2.33

x = 2.33 - 10

x = -7.66

Problem 17 :

(x − 5)⁴ = 256

Solution :

(x − 5)⁴ = 256

x - 5 = (256)^1/4 

x - 5 = (4 x 4 x 4 x 4)^1/4 

x - 5 = ((4)⁴)^1/4 

x - 5 = (4)^{4 x (1/4)}

x - 5 = 4

x = 4 + 5

x = 9

So, the value of x is 9.