SOLVE UNKNOWN VALUES IN EACH PARALLELOGRAM
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length.
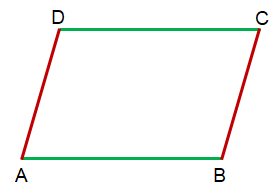
In the above figure, ABCD is a Parallelogram.
- If AB ∥ CD, then AB = CD
- If AD ∥ BC, then AD = BC
Find the value of x in each parallelogram.
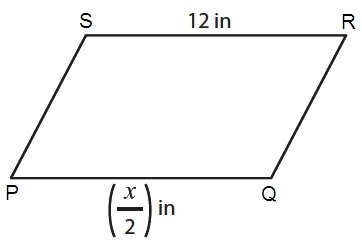
Problem 1 :
Solution :
By observing the figure,
PQ ∥ RS
So, PQ = RS (Opposite sides of parallel are equal)
Here PQ = x/2 in and RS = 12 in
(x/2) = 12
x = 12 × 2
x = 24 in2
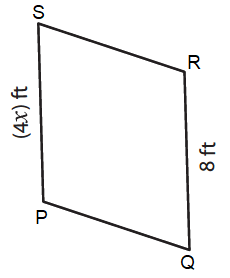
Problem 2 :
Solution :
By observing the figure,
PS ∥ QR
So, PS = QR (Opposite sides of parallel are equal)
Here PQ = 4x ft and RS = 8 ft
4x = 8
x = 8/4
x = 2 ft
Problem 3 :
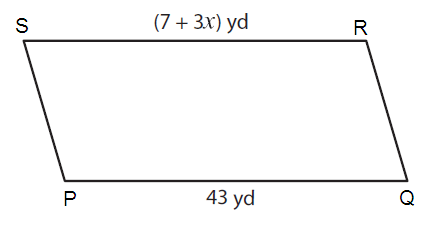
Solution :
By observing the figure,
PQ ∥ RS
So, PQ = RS (Opposite sides of parallel are equal)
Here PQ = 43 yd and RS = (7 + 3x) yd
43 = (7 + 3x)
Subtracting 7 on both sides.
43 - 7 = 7 + 3x - 7
36 = 3x
36/3 = x
12 yd = x
Problem 4 :
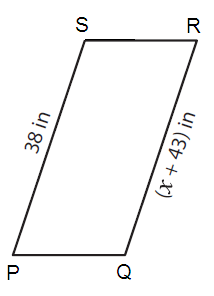
Solution :
By observing the figure,
PS ∥ QR
So, PS = QR (Opposite sides of parallel are equal)
Here PS = 38 in and QR = (x + 43) in
38 = (x + 43)
Subtracting 43 on both sides.
38 - 43 = x + 43 – 43
-5 in. = x
Find the value of x and y in each parallelogram.
Problem 5 :
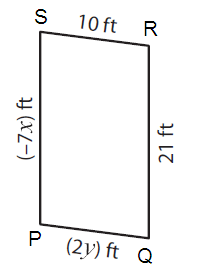
Solution :
By observing the figure,
PS ∥ QR and PQ ∥ RS
So, PS = QR and PQ = RS (Opposite sides of parallel are equal)
Here PS = (-7x)ft, QR = 21 ft, PQ = (2y)ft, and RS = 10 ft
-7x = 21 and 2y = 10
|
-7x = 21 -x = 21/7 -x = 3 x = -3 |
2y = 10 y = 10/2 y = 5 |
Therefore, x = -3 and y = 5.
Problem 6 :
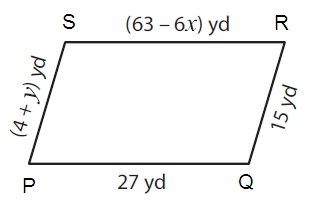
Solution :
By observing the figure,
PQ ∥ RS and PS ∥ QR
So, PQ = RS and PS = QR (Opposite sides of parallel are equal)
Here PQ = 27 yd, RS = (63 – 6x) yd, PS = (4 + y) yd, and QR = 15 yd
27 = (63 – 6x) and (4 + y) = 15
|
27 = 63 – 6x 27 – 63 = - 6x -36 = -6x x = 6 |
4 + y = 15 y = 15 - 4 y =11 |
Therefore, x = 6 and y = 11.
Problem 7 :
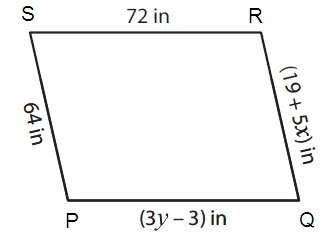
Solution :
By observing the figure,
PS ∥ QR and PQ ∥ RS
So, PS = QR and PQ = RS (Opposite sides of parallel are equal)
Here PS = 64 in, QR = (19 + 5x) in, PQ = (3y - 3) in, and RS = 72 in
64 = (19 + 5x) and (3y – 3) = 72
|
64 = 19 + 5x 64 – 19 = 5x 45 = 5x 9 = x |
3y – 3 = 72 3y = 72 + 3 3y = 75 y = 25 |
Therefore, x = 9 and y = 25.
Problem 8 :
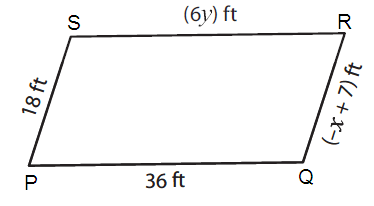
Solution :
By observing the figure,
PS ∥ QR and PQ ∥ RS
So, PS = QR and PQ = RS (Opposite sides of parallel are equal)
Here PS = 18 ft, QR = (-x + 7) ft, PQ = 36 ft, and RS = (6y) ft
18 = (-x + 7) and 36 = 6y
|
18 = -x + 7 18 – 7 = - x -11 = x |
36 = 6y (36)/6 = y 6 = y |
Therefore, x = -11 and y = 6.
Problem 9 :
For the parallelogram given below, find the value of x, y and z
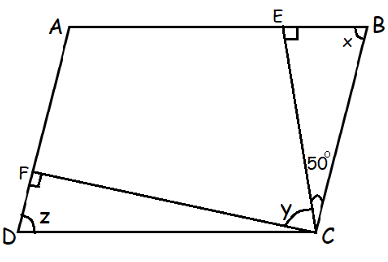
Solution :
In triangle BEC,
∠E + ∠B + ∠C = 180
90 + x + 50 = 180
140 + x = 180
x = 180 - 140
x = 40
z = 50
∠DFC = 90
∠DCF = ?
In triangle FDC,
∠FDC + ∠DCF + ∠CFD = 180
50 + ∠DCF + 90 = 180
∠DCF + 140 = 180
∠DCF = 180 - 140
∠DCF = 40
Sum of co-interior angle is 180 degree.
40 + y + 50 + x = 180
40 + y + 50 + 40 = 180
130 + y = 180
y = 180 - 130
y = 50
Problem 10 :
In a parallelogram PQRS, if ∠P = (3x − 5)° and ∠Q = (2x + 15)°, then find the value of x.
Solution :
∠P and ∠Q are co-interior angles, the sum of co-interior angles is 180.
3x - 5 + 2x + 15 = 180
5x + 10 = 180
5x = 180 - 10
5x = 170
x = 170 / 5
x = 34
Problem 11 :
In the given figure, ABCD is a parallelogram. Find x, y, z and p.
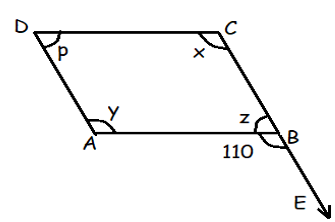
Solution :
110 + z = 180
z = 180 - 110
z = 70
y and z are co-interior angles.
y + z = 180
y + 70 = 180
y = 180 - 70
y = 110
p = 70 and y = x = 110
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling