SOLVE THE EQUATION BY FIRST CLEARING THE FRACTIONS

Problem 1 :

(1/2)t + (1/4) = 5/16

Solution :

Subtract 1/4 from both sides

(1/2)t + (1/4) – (1/4) = (5/16) – (1/4)

(1/2)t = 1/16

Multiply both sides by 2

(1/2t) (2) = (1/16) (2)

t = 1/8

Problem 2 :

(5/6s) + (2/9) = -7/12

Solution :

Subtract 2/9 from both sides

(5/6)s + (2/9) – (2/9) = (-7/12) – (2/9)

LCM of 12, 9 is 108

(5/6)s = (-87/108)

Multiply both sides by 6/5

(5/6)s (6/5) = (-87/108) (6/5)

s = -29/30

Problem 3 :

3/4 = (5/6)a + 2/9

Solution :

By Swap,

(5/6)a + 2/9 = 3/4

Subtract 2/9 from both sides

(5/6)a + (2/9) – (2/9) = (3/4) – (2/9)

LCM of 4, 9 is 36

(5/6)a = 19/36

Multiply both sides by 6/5

(5/6)a (6/5) = (19/36) (6/5)

a = 19/30

Problem 4 :

5/8 = (1/10) + (5/14)m

Solution :

By Swap,

(1/10) + (5/14)m = 5/8

Subtract 1/10 from both sides

(1/10) - (1/10) + (5/14)m = (5/8) – (1/10)

LCM of 8, 10 is 80

(5/14)m = 21/40

Multiply both sides by 14/5

(5/14)m (14/5) = (21/40) (14/5)

m = 147/100

Problem 5 :

(-41/60) + (17/20)p = 29/30

Solution :

Add 41/60 to both sides

(-41/60) + (41/60) + (17/20)p = (29/30) (41/60)

LCM of 30, 60 is 60

(17/20)p = 99/60

Multiply both sides by 20/17

(17/20)p (20/17) = (99/60) (20/17)

p = 33/17

Problem 6 :

3/8 = (-1/4)x – (3/5)

Solution :

(-1/4)x – (3/5) = 3/8

Add 3/5 to both sides

(-1/4)x – (3/5) + (3/5) = (3/8) + (3/5)

LCM of 8, 5 is 40

(-1/4)x = 39/40

Multiply both sides by -4

(-1/4)x (-4) = (39/40) (-4)

x = -39/10

Problem 7 :

(-3/2)t – (5/6) = -4/9

Solution :

Add 5/6 to both sides

(-3/2)t – (5/6) + (5/6) = (-4/9) + (5/6)

LCM of 9, 6 is 54

(-3/2)t = 7/18

Multiply both sides by -2/3

(-3/2)t (-2/3) = (7/18)(-2/3)

t = -7/27

Problem 8 :

(-3/5)z – 4 = -77/20

Solution :

Add 4 to both sides

(-3/5)z – 4 + 4 = (-77/20) + 4

(-3/5)z = 3/20

Multiply both sides by -5/3

(-3/5)z (-5/3) = (3/20) (-5/3)

z = -1/4

Problem 9 :

4w + (2/7) = -4/5

Solution :

Subtract 2/7 from both sides

4w + (2/7) – (2/7) = (-4/5) – (2/7)

LCM of 5, 7 is 35

4w = -38/35

Multiply both sides by 1/4

(4w) (1/4) = (-38/35) (1/4)

w = -19/70

Problem 10 :

On a test, you correctly answer six 5-point questions and eight 2-point questions. You earn 92% of the possible points on the test. How many points p is the test worth?

Solution :

Number of 5 point questions = 6, so 6 x 5 ==> 30

Number of 2 point questions = 8, so 2 x 8 ==> 16

Total = 30 + 16

= 46

Let p be number of points. By attending the questions you have recieved 92% of marks.

46 : p = 92 : 100

46/p = 92/100

Doing cross multiplication, we get

92p = 46(100)

p = 46(100)/92

p = 50

So, worth of the test is a total of 50 points.

Problem 11 :

A slush drink machine fills 1440 cups in 24 hours.

a. Write and solve an equation to find the number c of cups each symbol represents.

b. To lower costs, you replace the cups with paper cones that hold 20% less.

Write and solve an equation to find the number n of paper cones that the machine can fill in 24 hours.

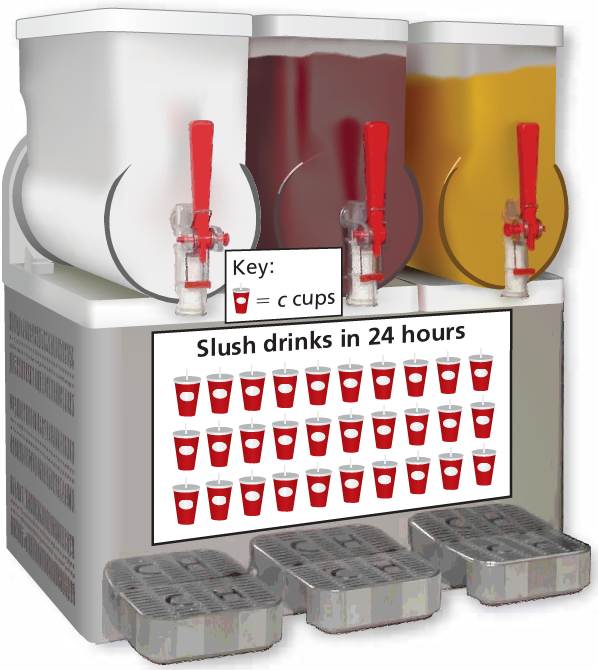
Solution :

a) Number of cups filled in 24 hours = 1440

Each symbol represents c cups. Number of symbols = 30

Total number of cups = 1440/30

= 48

So, each symbol will represent 48 cups.

b) Each paper cone will hold 80% of original quantity.

In 24 hours the machine can fill 1440 cups.

Number of cups filled in 1 hour = 1440/24

= 60 cups per hour

To find the number of paper cones, first calculate the volume of one paper cone:
Volume of one paper cone

= 60 cups * 0.8 = 48 cups/hour.

Now, divide the total number of cups by the volume of one paper cone to find the number of cones filled in 24 hours:

n = 1440 cups / 48 cups/hour

= 30 cones

Problem 11 :

Forty-five basketball players participate in a tournament. Write and solve an equation to find the number of 3-person teams that they can form.

Solution :

Number of basket player = 45

Let x be the number of teams which has 3 persons in each team.

3x = 45

x = 45/3

x = 15

So, there will be 15 teams.