SOLVE FOR X IN RELATIONS AND FUNCTIONS

Problem 1 :

If f(x) = √(3x – 20), what value of x does f(x) = 4 ?

Solution :

f(x) = √(3x – 20)

f(x) = 4

4 = √(3x – 20)

Squaring on both sides.

4² = (√(3x – 20))²

16 = 3x – 20

Add 20 on both sides.

16 + 20 = 3x

36 = 3x

Divide 3 on both sides.

12 = x

So, the value of x is 12.

Problem 2 :

If g(x) = √(5x + 19) + 20, what value of x does g(x) = 27 ?

Solution :

g(x) = √(5x + 19) + 20

g(x) = 27

27 = √(5x + 19) + 20

Subtract by 20 on both sides.

27 - 20 = √(5x + 19)

7 = √(5x + 19)

Squaring on both sides.

7² = (√(5x + 19))²

49 = 5x + 19

Subtract by 19 on both sides.

49 – 19 = 5x

30 = 5x

6 = x

So, the value of x is 6.

Problem 3 :

If h(x) = 2x³ – 19, what value of x does h(x) = 231?

Solution :

h(x) = 2x³ – 19

h(x) = 231

231 = 2x³ – 19

Add 19 on both sides.

231 + 19 = 2x³

250 = 2x³

125 = x³

x = 5

So, the value of x is 5.

Problem 4 :

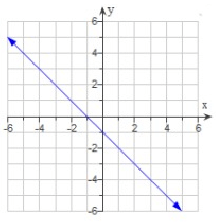
(a) Determine whether the graph illustrated represents a function.

(b) Give the domain and range of each function or relation in interval notations.

(c)  Approximate the value or values of x where y = 2.

Solution :

(a) Yes it is a function. Because if a vertical line is moved across the graph and, at any time, touches the graph at only one point, then the graph is a function.

(b)

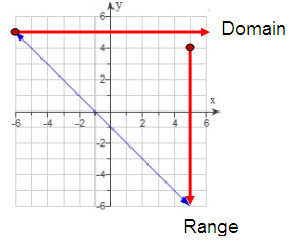
Domain D = (-∞, ∞), Range R = (-∞, ∞)

(c) By drawing the horizontal line through y = 2, the horizontal line is intersecting the given line at -3.

So, the value of x is -3, when y = 2.

Problem 5 :

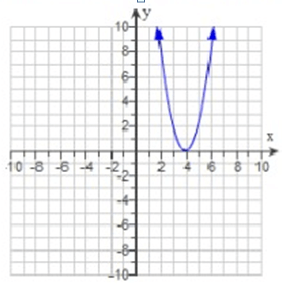
(a) Determine whether the graph illustrated represents a function.

(b) Give the domain and range of each function or relation in interval notations.

(c) Approximate the value or values of x where y = 2.

Solution :

(a) Yes it is a function. Because if a vertical line is moved across the graph and, at any time, touches the graph at only one point, then the graph is a function.

(b)  Domain D = (-∞, ∞), Range R = (0, ∞)

(c)  By drawing the horizontal line at y = 2, the horizontal line will intersect the curve at 3 and 5.

So, the points are (3, 2) (5, 2).

Problem 6 :

If G(x) = (2x + 3)/(x – 4) :

a. evaluate i G(2)  ii G(0)  iii G(-1/2)

b. find a value of x where G(x) does not exist.

c. find G(x + 2) in simplest form

d. find x if G(x) = -3.

Solution :

G(x) = (2x + 3)/(x – 4)

iii

G(-1/2) = (2(-1/2) + 3)/(-1/2 – 4)

= (-1 + 3) / [(-1 - 8)/2]

= 2 (-2/9)

= -4/9

b. By equating the denominator to 0, we get x - 4 = 0

x = 4. So, for 4 the function is undefined.

c. To find simplest form :

G(x) = (2x + 3)/(x – 4)

G(x + 2) = (2(x + 2) + 3)/((x + 2) – 4)

= (2x + 4 + 3)/(x + 2 – 4)

= (2x + 7)/(x – 2)

d. To find G(x) = -3

G(x) = (2x + 3)/(x – 4)

-3 = (2x + 3)/(x – 4)

Mutiplying (x – 4) on both sides.

-3(x – 4) = 2x + 3

-3x + 12 = 2x + 3

-5x = 3 – 12

-5x = -9

x = 9/5

Problem 7 :

If the value of a photocopier t years after purchase is given by V(t) = 9650 – 860t euros :

a. find V(4) and state what V(4) means

b. find t when V(t) = 5780 and explain what this represents

c. find the original purchase price of the photocopier.

Solution :

V(t) = 9650 – 860t

a.

V(4) = 860 × 4

= 3440

V(4) = 9650 – 3440

= 6210

V(4) means photocopier of 6210 Euros value after 4 years.

b.

V(t) = 5780

9650 – 860t = 5780

-860t = 5780 – 9650

-860t = -3870

t = 3870/860

t = 4.5

So, the value of t is 4.5, the time for the photocopier to reach a value of 5780 Euros.

c. The original purchase price of the photocopier is 9650 Euros.