SLOPES AND EQUATION OF LINE PRACTICE FOR SAT

Problem 1 :

2y + 3x = 5

2y - 3x = 5

Which of the following describes the graph of the system of equations above in the xy-plane.

(a)  A single line    (b) Two parallel lines

(c)  Two perpendicular lines

(d)  Two distinct intersecting lines they are not perpendicular.

Solution

Problem 2 :

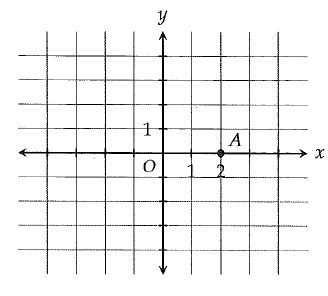
(i) Point B (not shown) is located by starting at A, moving 2 units down and moving 1 unit to the right. If a line is drawn through points A and B, what is the y-intercept of the line ?

(a)  1/2      (b)  1       (c)  2      (d)  4

(ii) Line l (not shown) contains point A and has a slope of 6. Which of the following points is on the line l.

(a)  (1, 6)      (b)  (2, 6)       (c)  (3, 6)      (d)  (6, 1)

Solution

Problem 3 :

The ordered pairs in the table above would form a line. Where would this line intersect the x-axis.

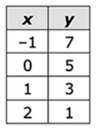
Problem 4 :

In the xy plane, a line has an x-intercept of -2 and the y-intercept of -4. What is the slope of the line ?

(a)  -2      (b)  -1/2       (c)  1/2      (d)  2

Solution

Problem 5 :

The graph of the function f contains the points (0, 3), (-2, 7) and (5, k). If the graph of f is a line. What must be the value of k ?

(a)  -13      (b)  -7       (c)  5      (d)  8

Solution

Problem 6 :

Line k has a negative slope and passes through the origin. If line m is perpendicular to like k, which of the following must be true ?

(a)  Line m passes through the origin.

(b) Line m does not pass through the origin.

(c)  Line m has a positive slope

(d)  Line m has negative slope

Solution

Problem 7 :

The graph of the line in the xy plane passes through points (0, 0) and (1, 2). The graph of the second line passes through points (1, 2) and (k, 0). If the two lines are perpendicular, what is the value of k ?                  Solution

Problem 8 :

Line m is graphed in the xy-plane. If an equation for line m is 6y + 2x = 5, which of the following statements is true ?

(a) Line m has slope of -3

(b) Line m has slope of 1/3

(c)  The x-intercept of the line m is 5/2 and the y-intercept is 5/6.

(d) The x-intercept of line m is 5/6 and the y-intercept is 5/2.

Solution