SKETCH THE REGION WHOSE AREA IS GIVEN BY THE DEFINITE INTEGRAL

Sketch the region whose area is given by the definite integral and evaluate the integral by

i) fundamental theorem of calculus

ii) using geometric formula

Problem 1 :

Solution :

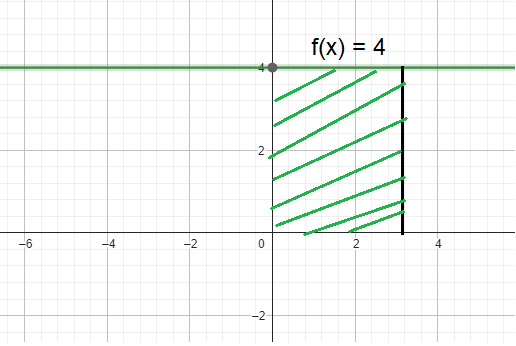
By evaluating the given integral, we can find the area of the shaded region shown above.

Using geometric formula :

By observing the shaded region, it is the shape of rectangle

length = 4, width = 3

Area of rectangle = length x width

= 4 x 3

= 12 square units.

Note :

In both ways, we will get the same answer.

Problem 2 :

Solution :

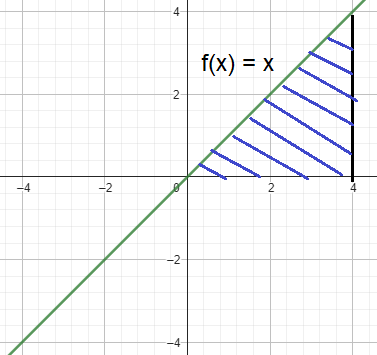
Using geometric formula :

By observing the shaded region, it is the shape of triangle

base = 4 and height = 4

Area of triangle = (1/2) x base x height

= (1/2) x 4 x 4

= 8 square units.

Problem 3 :

Solution :

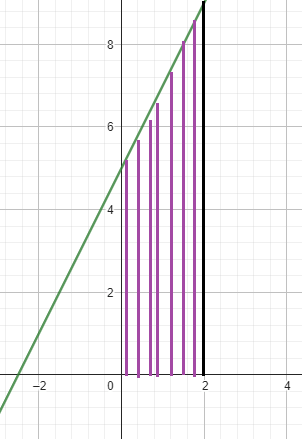
Using geometric formula :

By observing the shaded region, it is the shape of trapezium.

Let a and b are parallel sides and h be the height of the trapezium.

a = 5, b = 9 and h = 2

Area of trapezium = (1/2) x h(a + b)

= (1/2) x 2(5 + 9)

= 14 square units.

Problem 4 :

Solution :

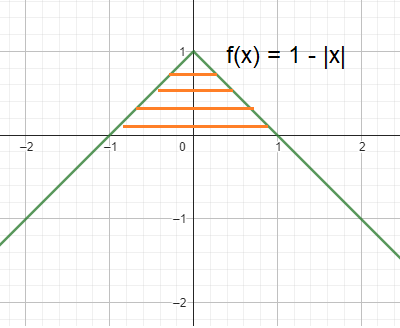
By observing the picture, the y-axis is dividing the given area into two symmetrical parts.

by redefining the absolute value function as piecewise function

Using geometric formula :

By observing the shaded region, it is the shape of triangle.

base = 2 and height = 1

Area of triangle = (1/2) x base x height

= (1/2) x 2 x 1

= 1 square unit

Problem 5 :

Solution :

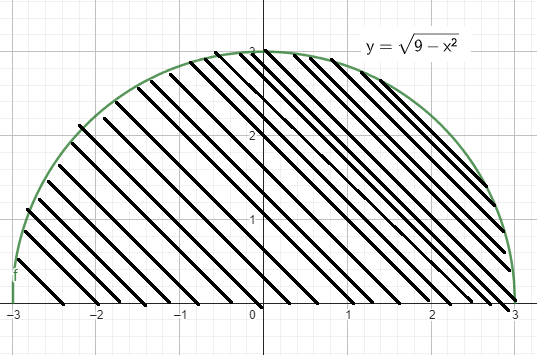
Using geometric formula :

By observing the shaded region, it is the shape of semicircle

radius = 3

Area of semicircle = (1/2) x πr²

= (1/2) x π x 3²

= 9π/2 square units

Problem 6 :

Solution :

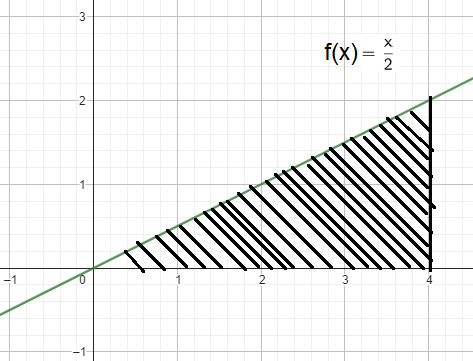
Using geometric formula :

By observing the shaded region, it is the shape of triangle.

base = 4 and height = 2

Area of triangle = (1/2) x base x height

= (1/2) x 4 x 2

= 4 square units