SKETCH THE GRAPH OF A FUNCTION WITH THE GIVEN PROPERTIES

In each case, sketch a graph of continuous function with the given properties.

Problem 1 :

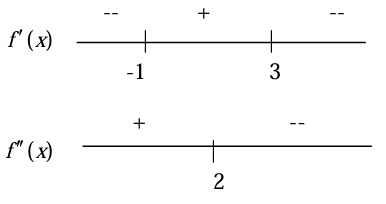
f'(-1) = 0 and f'(3) = 0

Solution :

From the first information, critical numbers are -1 and 3.

• f'(x) < 0 at the interval (-∞, -1)
• f'(x) > 0 at the interval (-1, 3)
• f'(x) < 0 at the interval (3, ∞)

From the above discussion,

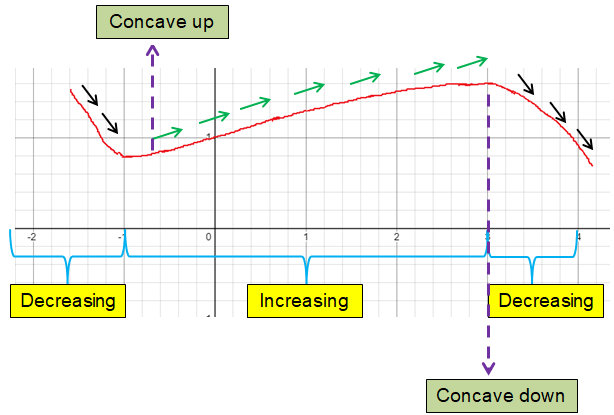
At the interval (-1, 3) is increasing. 

At the intervals (-∞, -1) U (3, ∞), the curve is decreasing.

From the given information,

• f''(x) > 0 at the interval (-∞, 2)
• f''(x) < 0 at the interval (2, ∞)

From the above discussion,

At the interval (-∞, 2), it is concave up.

At the interval (2, ∞), it is concave down.

Problem 2 :

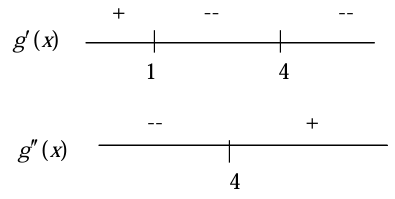
g'(1) = 0 and g'(3) is undefined.

Solution :

From the first information, critical numbers are 1 and 3. At x = 3, the curve f(x) will be sharpen.

• f'(x) > 0 at the interval (-∞, 1)
• f'(x) < 0 at the interval (1, 4)
• f'(x) < 0 at the interval (4, ∞)

From the above discussion,

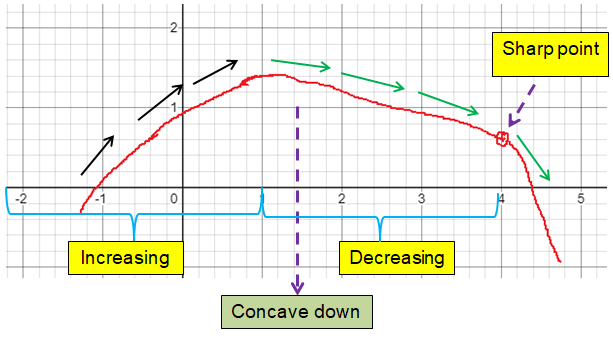
At the interval (-∞, 1) is increasing. 

At the intervals (1, 4) U (4, ∞), the curve is decreasing.

From the given information,

• f''(x) < 0 at the interval (-∞, 4)
• f''(x) > 0 at the interval (4, ∞)

From the above discussion,

At the interval (-∞, 4), it is concave down.

At the interval (4, ∞), it is concave up.

Problem 3 :

h'(-2) = 0, h'(2) = 0 and h'(0) is undefined.

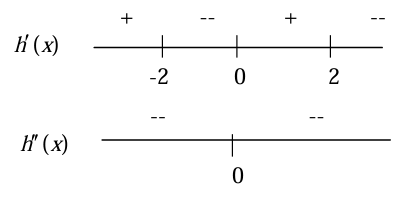
Solution :

From the first information, critical numbers are -2, 2 and 0. At x = 0, the curve f(x) will be sharpen.

• f'(x) > 0 at the interval (-∞, -2)
• f'(x) < 0 at the interval (-2, 0)
• f'(x) > 0 at the interval (0, 2)
• f'(x) < 0 at the interval (2, ∞)

From the above discussion,

At the intervals  (-∞, -2) and (0, 2) is increasing. 

At the intervals  (-2, 0) U (2, ∞), the curve is decreasing.

From the given information,

• f''(x) < 0 at the interval (-∞, ∞)

From the above discussion,

At the interval (-∞, ∞), it is concave down. 

Problem 3 :

f(x) = (8x - 16) / x²

Solution :

f(x) = (8x - 16) / x²

Using quotient rule, we find the first derivative.

f'(x) = (vu' - uv') / v²

= (x²(8) - (8x - 16)(2x)) / (x²)²

= (8x²- (16x² - 32x)) / x⁴

= (8x²- 16x² + 32x) / x⁴

f'(x) = (-8x² + 32x) / x⁴

f'(x) = 0

(-8x² + 32x) / x⁴ = 0

-8x² + 32x = 0

-4x(2x - 8) = 0

4x = 0 and 2x - 8 = 0

x = 0 and 2x = 8 ==> x = 4

So, the critical points are 0 and 4.

Problem 4 :

f(x) = 2x + 3x^2/3

Solution :

f(x) = 2x + 3x^2/3

f'(x) = 2(1) + 3(2/3)x^{(2/3) - 1}

f'(x) = 2 + 2x^(-1/3)

f'(x) = 0

2 + 2x^(-1/3) = 0

2x^(-1/3) = -2

x^(-1/3) = -1

1/∛x = -1

∛x = -1

x = -1

So, the critical point is at x = -1.

Problem 5 :

f(x) = x⁴ - 2x² + 3

Solution :

f(x) =  x⁴ - 2x² + 3

f'(x) = 4x³ - 2(2x) + 0

= 4x³ - 4x

f'(x) = 0

4x³ - 4x = 0

4x(x² - 1) = 0

4x = 0 and x² - 1 = 0

x = 0 and x² = 1

x = 1 and -1

So, the critical points are -1, 0 and 1.