SINUSOIDAL FUNCTION TRANSFORMATIONS

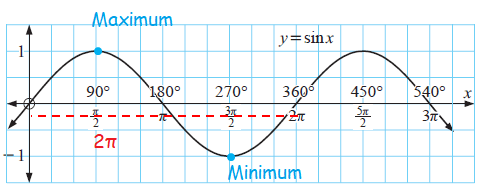
Amplitude Period Maximum and Minimum of Sine Functions

A periodic function is one which repeats itself over and over in horizontal direction.

What is period ?

The period of a periodic function is the length of one repetition or cycle

What is amplitude ?

The amplitude is the vertical distance between a maximum point and the principal axis.

What is maximum and minimum ?

• The maximum points occurs at the top of the crest.
• The minimum points occurs at the bottom of a through.

What is principal axis or man line ?

The graph oscillates about horizontal line called the principal axis or mean line.

y = a sin (k(x - d)) + c

y = a cos (k(x - d)) + c

• The amplitude is |a|
• Period is 2π/|k|

Problem 1 :

The graph of the sinusoidal function ℎ is shown in the figure above. The function ℎ can be written as h(θ) = a sin (bθ) + d. Find the values of the constants a, b, and d.

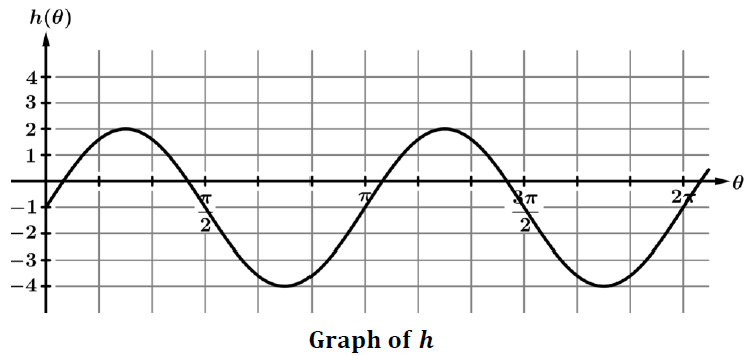
Solution :

Let us consider the sin function in the form 

y = a sin (k(x - d)) + c

First let us draw the midline or axis of symmetry of the sine curve. 

y = -1

The first cycle appears in the interval [0, π]

Period = π

2π/|k| = π

|k| = 2π/π

|k| = 2

Height of the graph = 2

a = 2

• No translation horizontally, then d = 0
• Vertical translation of 1 unit down, then c = -1

y = 2 sin (2(x - 0)) + 0

y = 2 sin 2x

The required function will be,

h(θ) = 2 sin (2θ)

Problem 2 :

The graph of the sinusoidal function 𝑓 is shown in the figure above. The function 𝑓 can be written as 

f(θ) = a sin (bθ) + d

Find the values of the constants a, b, and d.

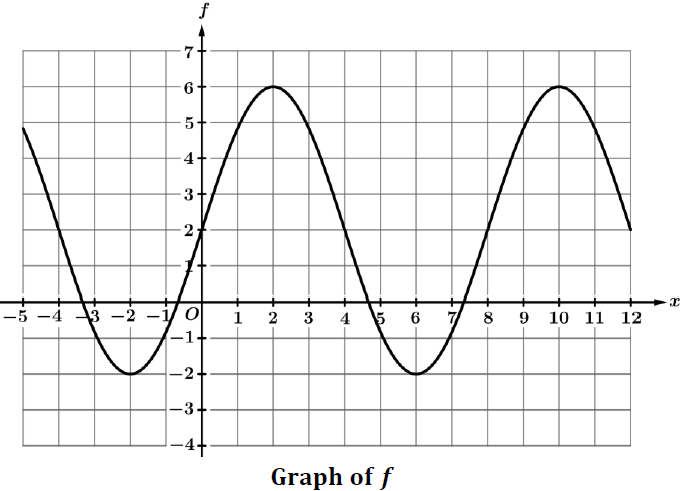
Solution :

Let us consider the sin function in the form 

y = a sin (k(x - d)) + c

First let us draw the midline or axis of symmetry of the sine curve. 

y = 2

The first cycle appears in the interval [0, 8]

Period = 8

2π/|k| = 8

|k| = 2π/8

|k| = 2π/8

|k| = π/4

Height of the graph = 4 (distance from midline to the maximum point)

a = 4

• No translation horizontally, then d = 0
• Vertical translation of 2 unit up, then c = 2

y = 4 sin ( π/4(x - 0)) + 2

y = 4 sin (πx/4) + 2

The required function will be,

h(θ) = 4 sin (πθ/4) + 2

Problem 3 :

The graph of the sinusoidal function 𝑔 is shown in the figure above. The function 𝑔 can be written as

g(θ) = a sin (bθ) + d

Find the values of the constants a, b, and d.

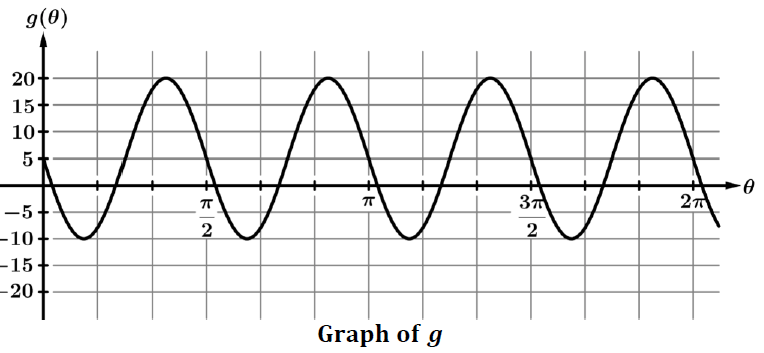
Solution :

Let us consider the sin function in the form 

y = a sin (k(x - d)) + c

First let us draw the midline or axis of symmetry of the sine curve. 

y = 5

The first cycle appears in the interval [0, π/2]

Period = π/2

2π/|k| = π/2

|k| = 2π/(π/2)

|k| = 4π/π

|k| = 4

Height of the graph = 15 (distance from midline to the maximum point)

a = 15

• No translation horizontally, then d = 0
• Vertical translation of 5 units up, then c = 5
• There is reflection about x-axis.

y = -15 sin (4(x - 0)) + 5

y = -15 sin 4x + 5

The required function will be,

h(θ) = -15 sin (4θ)

Problem 4 :

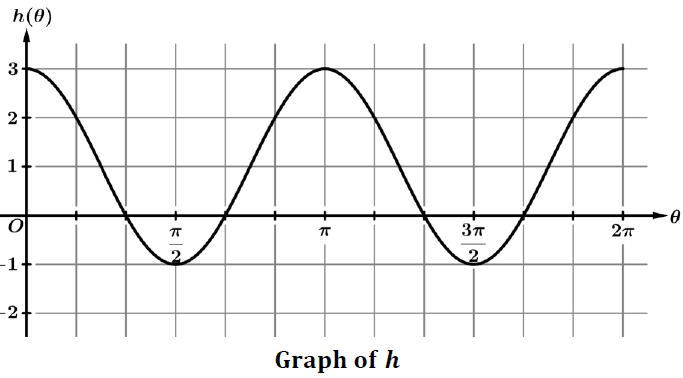
The figure shows the graph of a sinusoidal function ℎ. What are the values of the period and amplitude of ℎ?

a) The period is 𝜋, and the amplitude is 2.

b) The period is 𝜋, and the amplitude is 4.

c) The period is 2𝜋, and the amplitude is 2.

d) The period is 2𝜋, and the amplitude is 4.

Solution :

By observing the graph, it is the graph of cosine function. The first cycle appears at [0, π]. so, the period is π.

y = 1 is the midline

Height of the graph = 2

So, option a is correct.

Problem 5 :

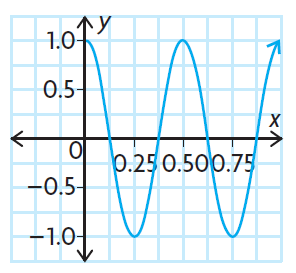
Solution :

By observing the graph, it must be the graph of cosine function.

y = a cos (k(x - d)) + c

First let us draw the midline or axis of symmetry of the cosine curve. 

y = 0

The first cycle appears in the interval [0, 0.5]

Period = 0.5 or 1/2

2π/|k| = 1/2

|k| = 2π/(1/2)

|k| = 4π

Height of the graph = 1 (distance from midline to the maximum point)

a = 1

• No translation horizontally, then d = 0
• No vertical translation, then c = 0

y = 1 cos (4π(x - 0)) + 0

y = cos 4πx

Problem 6 :

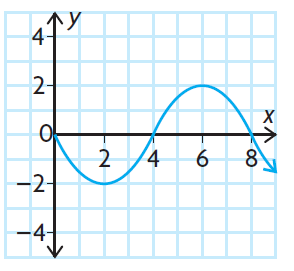
Solution :

By observing the graph, it must be the graph of sin function.

y = a sin (k(x - d)) + c

First let us draw the midline or axis of symmetry of the sin curve. 

y = 0

The first cycle appears in the interval [0, 8]

Period = 8

2π/|k| = 8

|k| = 2π/8

|k| = π/4

Height of the graph = 1 (distance from midline to the maximum point)

a = 2

• No translation horizontally, then d = 0
• No vertical translation, then c = 0
• Reflection across x-axis.

y = -2 sin (π/4(x - 0)) + 0

y = -2 sin (πx/4)